
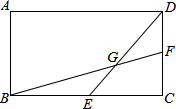
 如圖所示,長方形ABCD的長為a,寬為b,E、F分別為BC和CD的中點,連接BF、DE交于點G,則四邊形ABGD的面積為$\frac{2}{3}$ab.
如圖所示,長方形ABCD的長為a,寬為b,E、F分別為BC和CD的中點,連接BF、DE交于點G,則四邊形ABGD的面積為$\frac{2}{3}$ab. 分析 連接EF、BD、AG,作GM⊥AB于M,作GN⊥AD于N,證明EF是△BCD的中位線,得出EF∥BD,EF=$\frac{1}{2}$BD,得出GM=$\frac{2}{3}$BC=$\frac{2}{3}$a,同理:GN=$\frac{2}{3}$b,四邊形ABGD的面積=△ABG的面積+△ADG的面積,即可得出結果.
解答 解:連接EF、BD、AG,作GM⊥AB于M,作GN⊥AD于N,如圖所示: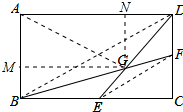
∵E、F分別為BC和CD的中點,
∴EF是△BCD的中位線,
∴EF∥BD,EF=$\frac{1}{2}$BD,
∴GF:BG=1:2,
∴BG:BF=2:3,
∴GM=$\frac{2}{3}$BC=$\frac{2}{3}$a,
同理:GN=$\frac{2}{3}$b,
∴四邊形ABGD的面積=△ABG的面積+△ADG的面積=$\frac{1}{2}$×b×$\frac{2}{3}$a+$\frac{1}{2}$×a×$\frac{2}{3}$b=$\frac{2}{3}$ab.
點評 本題考查了矩形的性質、三角形中位線定理、三角形面積的計算;熟練掌握矩形的性質,證明三角形中位線是解決問題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
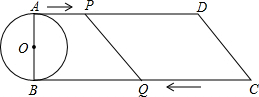 如圖,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB為⊙O的直徑,動點P從點A開始沿AD邊向點D以1cm/s的速度運動,動點Q從點C開始沿CB邊向點B以3cm/s速度運動.P、Q分別從點A、C同時出發,當其中一點到達終點時,另一點也隨之停止運動,設運動時間為t s,問:
如圖,已知直角梯形ABCD中,AD∥BC,∠B=90°,AB=8cm,AD=24cm,BC=26cm,AB為⊙O的直徑,動點P從點A開始沿AD邊向點D以1cm/s的速度運動,動點Q從點C開始沿CB邊向點B以3cm/s速度運動.P、Q分別從點A、C同時出發,當其中一點到達終點時,另一點也隨之停止運動,設運動時間為t s,問:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com