
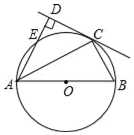
 如圖,AB為⊙O的直徑,C為⊙O上一點(diǎn),AD和過(guò)C點(diǎn)的切線互相垂直,垂足為D,AD交⊙O于點(diǎn)E,連接CE,CB
如圖,AB為⊙O的直徑,C為⊙O上一點(diǎn),AD和過(guò)C點(diǎn)的切線互相垂直,垂足為D,AD交⊙O于點(diǎn)E,連接CE,CB分析 (1)由切線性質(zhì)得:OC⊥CD,則OC∥AD,由平行線性質(zhì)和同圓半徑相等可證得:∠CAD=∠OAC,所以圓周角相等,則所對(duì)的弦相等,則CE=CB;
(2)證明△DEC∽△DCA,列比例式可求AD的長(zhǎng),利用勾股定理求AC的長(zhǎng),再證明△ADC∽△ACB,得AB的長(zhǎng),所以半徑為$\frac{13}{4}$.
解答  (1)證明:如圖,連接OC,
(1)證明:如圖,連接OC,
∵CD是⊙O的切線,
∴OC⊥CD,
又AD⊥CD,
∴OC∥AD,
∴∠ACO=∠CAD,
∵OC=OA,
∴∠ACO=∠OAC,
∴∠CAD=∠OAC
∴CE=CB;
(2)∵AB是⊙O的直徑,
∴∠ACB=90°,
∵AD⊥CD,
∴∠ADC=90°,
∴∠ADC=∠ACB,
∵∠DEC=∠B,
∴△DEC∽△CBA,
∵∠DAC=∠BAC,
∴△CBA∽△DCA,
∴△DEC∽△DCA,
∴$\frac{DE}{DC}=\frac{DC}{AD}$,
∴$\frac{2}{3}=\frac{3}{AD}$,
∴AD=$\frac{9}{2}$,
由勾股定理得:AC=$\sqrt{{3}^{2}+(\frac{9}{2})^{2}}$=$\sqrt{\frac{117}{4}}$,
∵△ADC∽△ACB,
∴$\frac{AC}{AB}=\frac{AD}{AC}$,
∴AC2=AD•AB,
∴$\frac{117}{4}$=$\frac{9}{2}$AB,
∴AB=$\frac{13}{2}$,
∴⊙O的半徑為$\frac{13}{4}$.
點(diǎn)評(píng) 本題考查了切線的性質(zhì)、圓周角定理、勾股定理等性質(zhì)的應(yīng)用,圓的切線垂直于過(guò)切點(diǎn)的半徑,在圓中,常利用同圓的半徑相等,并根據(jù)等邊對(duì)等角證明兩角相等;因此做好本題的關(guān)鍵是熟練掌握?qǐng)A中的性質(zhì),另外還要知道在圓中常用的輔助線的作法:①連接半徑,②作弦心距等.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 如圖△AOB和△COD均為直角三角形,且∠AOB=∠DOC=90°,其中∠ABO=∠DCO=30°,若BO=3$\sqrt{3}$,點(diǎn)N在線段OD上,且NO=2.點(diǎn)P是線段AB上的一個(gè)動(dòng)點(diǎn),在將△AOB繞點(diǎn)O旋轉(zhuǎn)的過(guò)程中,線段PN長(zhǎng)度的最小值為$\frac{3\sqrt{3}}{2}$-2.
如圖△AOB和△COD均為直角三角形,且∠AOB=∠DOC=90°,其中∠ABO=∠DCO=30°,若BO=3$\sqrt{3}$,點(diǎn)N在線段OD上,且NO=2.點(diǎn)P是線段AB上的一個(gè)動(dòng)點(diǎn),在將△AOB繞點(diǎn)O旋轉(zhuǎn)的過(guò)程中,線段PN長(zhǎng)度的最小值為$\frac{3\sqrt{3}}{2}$-2.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
| 第一天 | 第二天 | 第三天 | 第四天 | 第五天 | 第六天 | 第七天 | |
| 路程(km) | -8 | -11 | -14 | 0 | -16 | +41 | +8 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
 如圖,一次函數(shù)y=kx+b的圖象與反比例函數(shù)y=$\frac{m}{x}$的圖象交于A(-3,1)、B(2,n)兩點(diǎn).
如圖,一次函數(shù)y=kx+b的圖象與反比例函數(shù)y=$\frac{m}{x}$的圖象交于A(-3,1)、B(2,n)兩點(diǎn).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
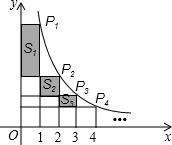 如圖,在反比例函數(shù)的圖象$y=\frac{4}{x}$(x>0)上,有點(diǎn)P1,P2,P3,P4,…,點(diǎn)P1橫坐標(biāo)為2,且后面每個(gè)點(diǎn)的橫坐標(biāo)與它前面相鄰點(diǎn)的橫坐標(biāo)的差都是2,過(guò)點(diǎn)P1,P2,P3,P4,…分別作x軸,y軸的垂線,圖中所構(gòu)成的陰影部分的面積從左到右依次為S1,S2,S3,…則S1+S2+S3+…+Sn=4-$\frac{4}{n+1}$.
如圖,在反比例函數(shù)的圖象$y=\frac{4}{x}$(x>0)上,有點(diǎn)P1,P2,P3,P4,…,點(diǎn)P1橫坐標(biāo)為2,且后面每個(gè)點(diǎn)的橫坐標(biāo)與它前面相鄰點(diǎn)的橫坐標(biāo)的差都是2,過(guò)點(diǎn)P1,P2,P3,P4,…分別作x軸,y軸的垂線,圖中所構(gòu)成的陰影部分的面積從左到右依次為S1,S2,S3,…則S1+S2+S3+…+Sn=4-$\frac{4}{n+1}$.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com