
| 用水量 | 單價 |
| 0<x≤22 | a |
| 剩余部分 | a+1.1 |
分析 (1)由單價=總價÷數量就可以得出結論;
(2)設該用戶2月份水費=0<x≤22的水費+x大于22部分的水費,列出算式計算即可求解;
(3)設該用戶3月份實際用水m噸,由70%的水量的水費為71元=單價×數量建立方程求出其解即可.
解答 解:(1)a=23÷10=2.3(元/m3);
(2)2.3×22+(2.3+1.1)×(25-22)
=50.6+3.4×3
=50.6+10.2
=60.8(元).
答:需交水費60.8元;
(3)設該用戶實際用水m立方米,由題意,得
2.3×22+(2.3+1.1)×(70%m-22)=71,
解得:m=$\frac{250}{7}$.
故該用戶實際用水$\frac{250}{7}$立方米.
故答案為:2.3;$\frac{250}{7}$.
點評 本題考查了單價×數量=總價的數量關系的運用,列一元一次方程解實際問題的運用,一元一次方程的解法的運用,解答時由單價×數量=總價的關系建立方程是關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
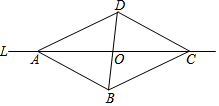 如圖,△ABC沿直線L對折后能與△ADC重合,且AB∥CD,下列選項正確的是( )
如圖,△ABC沿直線L對折后能與△ADC重合,且AB∥CD,下列選項正確的是( )| A. | AB=CD,AO=OC | B. | AB=BD,∠BAD=∠DCB | C. | AB∥BC,BC=BD | D. | OD=OB,∠CDB=∠BCD |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\sqrt{25}=±5$ | B. | $\sqrt{(-7)^{2}=-7}$ | C. | |4-3$\sqrt{2}$|=3$\sqrt{2}$-4 | D. | ($\sqrt{2}+1$)2=3 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 如圖,△OAB與△OCD是以點O為位似中心的位似圖形,相似比為1:2,∠OCD=90°,CO=CD.若B(1,0),則點C的坐標為( )
如圖,△OAB與△OCD是以點O為位似中心的位似圖形,相似比為1:2,∠OCD=90°,CO=CD.若B(1,0),則點C的坐標為( )| A. | (1,1) | B. | (1,2) | C. | ($\sqrt{2}$,$\sqrt{2}$) | D. | (2,1) |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com