
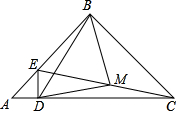
 已知在△ABC中,∠ABC=90°,AB=BC=8cm,點D為AC一點,過點D作DE⊥AC交線段AB于點E,點M為EC的中點.
已知在△ABC中,∠ABC=90°,AB=BC=8cm,點D為AC一點,過點D作DE⊥AC交線段AB于點E,點M為EC的中點.分析 (1)根據(jù)直角三角形斜邊上的中線等于斜邊的一半可得BM=$\frac{1}{2}$CE,DM=$\frac{1}{2}$CE,得出BM=DM,再由等腰三角形的性質(zhì)和三角形的外角性質(zhì)證出∠BMD=90°即可;
(2)過B作BF⊥DE交DE的延長線于F,推出△BEF是等腰直角三角形,根據(jù)勾股定理得到AE=$\sqrt{2}$AD=2cm,BF=3$\sqrt{2}$cm,CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=10cm,根據(jù)三角形的面積即刻得到結(jié)論.
解答 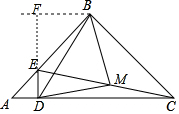 (1)證明:∵DE⊥AC,
(1)證明:∵DE⊥AC,
∴∠EDC=90°,
∵∠ABD=90°,點M為EC的中點,
∴DM=BM=CM,
∴∠MBC=∠BCM,∠MCD=∠MDC,
∵∠BME=∠MBC+∠BCM,∠DME=∠MCD+∠MDC,
∴∠BMD=∠BME+∠DME=2∠ACB=90°,
∴△BMD為等腰直角三角形;
(2)過B作BF⊥DE交DE的延長線于F,
∵∠ADE=90°,∠A=45°,
∴∠FEB=∠AED=45°,
∴△BEF是等腰直角三角形,
∵AD=$\sqrt{2}$cm,∴AE=$\sqrt{2}$AD=2cm,
∴BE=6cm,∴BF=3$\sqrt{2}$cm,
∴CE=$\sqrt{B{E}^{2}+B{C}^{2}}$=10cm,
∴DM=BM=5cm,
∴四邊形BEDM的面積=S△BEM+S△BDE=$\frac{1}{2}×$5×5+$\frac{1}{2}$×$\sqrt{2}$×3$\sqrt{2}$=15.5cm2.
點評 本題考查了等腰直角三角形的判定和性質(zhì),直角三角形的性質(zhì),三角形的面積的計算,正確的作出輔助線是解題的關(guān)鍵.


 名校課堂系列答案
名校課堂系列答案科目:初中數(shù)學 來源: 題型:解答題
 太極圖的形狀為陰陽兩魚互糾在一起(如圖),象征兩極和合.太極圖中的白色部分作怎樣的變換,可得到黑色部分?若整個圓的直徑為6cm,求出圖中黑色部分的面積?
太極圖的形狀為陰陽兩魚互糾在一起(如圖),象征兩極和合.太極圖中的白色部分作怎樣的變換,可得到黑色部分?若整個圓的直徑為6cm,求出圖中黑色部分的面積?查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
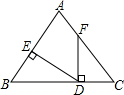 如圖,點D在邊BC上,DE⊥AB,DF⊥BC,垂足分別為點E、D,BD=CF,BE=CD.若∠AFD=140°,則∠EDF=50°.
如圖,點D在邊BC上,DE⊥AB,DF⊥BC,垂足分別為點E、D,BD=CF,BE=CD.若∠AFD=140°,則∠EDF=50°.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | $\sqrt{2}$$+\sqrt{2}$=2 | B. | 3+$\sqrt{2}$=3$\sqrt{2}$ | C. | $\sqrt{3}$+$\sqrt{2}$=$\sqrt{5}$ | D. | $\sqrt{9}$+$\sqrt{3}$=3$+\sqrt{3}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | x=2 | B. | x≠2 | C. | $x=\frac{3}{2}$ | D. | $x≠\frac{3}{2}$ |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com