Question

8．如圖，平面直角坐標系的原點O是正方形A′B′C′D′的中心，把正方形A′B′C′D′繞原點O順時針旋轉45°得正方形ABCD，且頂點A、B的坐標分別為（1，1）、（-1，1），則正方形A′B′C′D′與正方形ABCD重疊部分所形成的正八邊形的周長為16$\sqrt{2}$-16．

Answer 1

分析 如圖，首先求出正方形的邊長、對角線長；進而求出OA′的長；證明△A′MN為等腰直角三角形，求出A′N的長度；同理求出D′M′的長度，即可解決問題．

解答 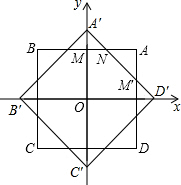解：如圖，由題意得：
正方形ABCD的邊長為2，
∴該正方形的對角線長為2$\sqrt{2}$，
∴OA′=$\sqrt{2}$；而OM=1，
∴A′M=$\sqrt{2}$-1；
由題意得：∠MA′N=45°，∠A′MN=90°，
∴∠MNA′=45°，
∴MN=A′M=$\sqrt{2}$-1；
由勾股定理得：A′N=2-$\sqrt{2}$；
同理可求D′M′=2-$\sqrt{2}$，
∴NM'=2-（4-2$\sqrt{2}$）=2$\sqrt{2}$-2，
∴正八邊形的邊長為2$\sqrt{2}$-2，
∴正八邊形的周長=（2$\sqrt{2}$-2）×8=16$\sqrt{2}$-16．
故答案為：16$\sqrt{2}$-16．

點評 該題主要考查了旋轉變換的性質、正方形的性質、勾股定理等幾何知識點及其應用；應牢固掌握旋轉變換的性質、正方形的性質等幾何知識點，這是靈活運用、解題的基礎和關鍵．