

分析 (1)分兩種情形討論即可解決問題.
(2)想辦法證明FM=GN,MN2=FM2+NG2即可.
(3)結論:yD=2yC.如圖3中,由題意拋物線L1的解析式為y=-2(x-x1)(x-x2),根據對稱軸為x=$\frac{{x}_{1}+{x}_{2}}{2}$,求出yC,因為點M,N是線段AB的和諧分割點切MN>AM,所以MN=$\sqrt{2}$AM=$\sqrt{2}$(x2-x1),所以N[x2+$\sqrt{2}$(x2-x1),0],推出拋物線L2的解析式為y=-2(x-x2)[x-x2-$\sqrt{2}$(x2-x1)],根據對稱軸為x=$\frac{{2x}_{2}+\sqrt{2}({x}_{2}-{x}_{1})}{2}$,求出yD即可解決問題.
(4)如圖4中,將△ABM繞點A旋轉得到△ADP,連接PN,首先證明△ANP≌△ANM,推出MN=PN,BM=PD,因為M,N是線段BD的和諧分割點,所以△PDN是等腰直角三角形,推出∠PDN=45°或90°,分別討論即可.
解答 解:(1)如圖1中,當MN是斜邊時,MN=4$\sqrt{2}$,當MN是直角邊時,MN=4或2$\sqrt{2}$,
故答案為4$\sqrt{2}$或4或2$\sqrt{2}$.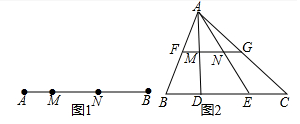
(2)如圖2中,由題意DE2=BD2+EC2,BD=EC,
∵FG∥BC,
∴$\frac{FM}{BD}$=$\frac{AF}{AB}$=$\frac{AG}{AC}$=$\frac{NG}{EC}$,$\frac{MN}{ED}$=$\frac{AM}{AD}$=$\frac{AF}{AB}$,
∴FM=NG,$\frac{FM}{BD}$=$\frac{MN}{DE}$=$\frac{NG}{EC}$,設,$\frac{FM}{BD}$=$\frac{MN}{DE}$=$\frac{NG}{EC}$=$\frac{1}{k}$,
∴BD=k•FM,DE=k•MN,EC=k•NG,
∴k2•MN2=k2•BD2+k2•NG2,
∴MN2=FM2+GN2,
∴以FM,MN,GN為邊的三角形是一個等腰直角三角形.
∴M,N是線段FG的和諧分割點.
(3)結論:yD=2yC.理由如下,
如圖3中,由題意拋物線L1的解析式為y=-2(x-x1)(x-x2),
∵對稱軸為x=$\frac{{x}_{1}+{x}_{2}}{2}$,
∴yC=-2($\frac{{x}_{1}+{x}_{2}}{2}$-x1)($\frac{{x}_{1}+{x}_{2}}{2}$-x2)=$\frac{({x}_{2}-{x}_{1})^{2}}{2}$,
∵點M,N是線段AB的和諧分割點切MN>AM,
∴MN=$\sqrt{2}$AM=$\sqrt{2}$(x2-x1),
∴N[x2+$\sqrt{2}$(x2-x1),0],
∴拋物線L2的解析式為y=-2(x-x2)[x-x2-$\sqrt{2}$(x2-x1)],
∵對稱軸為x=$\frac{{2x}_{2}+\sqrt{2}({x}_{2}-{x}_{1})}{2}$,∴yD=-2[$\frac{2{x}_{2}+\sqrt{2}({x}_{2}-{x}_{1})}{2}$-x2][$\frac{2{x}_{2}+\sqrt{2}({x}_{2}-{x}_{1})}{2}$-x2-$\sqrt{2}$(x2-x1)=(x2-x1)2,
∴yD=2yC.
(4)如圖4中,將△ABM繞點A旋轉得到△ADP,連接PN.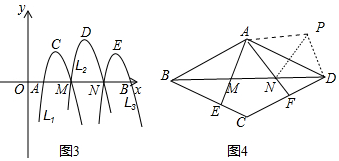
∵∠MAN=$\frac{1}{2}$∠BAD,
∴∠BAM+∠DAN=$\frac{1}{2}$∠BAD=∠DAN+∠PAD,
∴∠PAN=∠NAM,∵AN=AN,AM=AP,
∴△ANP≌△ANM,
∴MN=PN,BM=PD,
∵M,N是線段BD的和諧分割點,
∴△PDN是等腰直角三角形,
∴∠PDN=45°或90°,
當∠PDN=90°時,∠ADP=∠ADN=∠ABD=45°,
∵四邊形ABCD是菱形,
∴∠ABC=2∠ABD=90°,不合題意,
∴∠PDN=45°,
∴∠ADP=∠ADB=∠ABD=22.5°,
∠ABC=2∠ABD=45°,
∴β=45°,sinβ=$\frac{\sqrt{2}}{2}$.
點評 本題考查二次函數綜合題、平行線分線段成比例定理、菱形的性質、全等三角形的判定和性質、勾股定理等知識,解題的關鍵是理解題意,學會利用參數解決問題,學會添加常用輔助線,構造全等三角形解決問題,學會用分類討論的思想思考問題,屬于中考壓軸題.


科目:初中數學 來源: 題型:選擇題
| A. | 如果x1、x2同號.那么點P、Q在同一象限 | |
| B. | 如果y1、y2異號.那么點P、Q在不同象限 | |
| C. | 如果k>0.且x1>x2,那么y1<y2 | |
| D. | 如果k<0.且x1<0,x2>0,那么y1>y2 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知△ABC.
如圖,已知△ABC.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
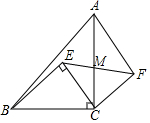 如圖,等腰直角△ABC中,∠ACB=90°,點E為△ABC內一點,且∠BEC=90°,將△BEC繞C點順時針旋轉90°,使BC與AC重合,得到△AFC,連接EF交AC于點M,已知BC=10,CF=6,則AM:MC的值為( )
如圖,等腰直角△ABC中,∠ACB=90°,點E為△ABC內一點,且∠BEC=90°,將△BEC繞C點順時針旋轉90°,使BC與AC重合,得到△AFC,連接EF交AC于點M,已知BC=10,CF=6,則AM:MC的值為( )| A. | 4:3 | B. | 3:4 | C. | 5:3 | D. | 3:5 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com