
 如圖,AB、CD為⊙O的直徑,弦AE∥CD,連接BE交CD于點F,過點E作直線EP與CD的延長線交于點P,使∠PED=∠C.
如圖,AB、CD為⊙O的直徑,弦AE∥CD,連接BE交CD于點F,過點E作直線EP與CD的延長線交于點P,使∠PED=∠C.分析 (1)連接OE,如圖,利用圓周角定理得到∠CED=90°,即∠CEO+∠OED=90°,加上∠C=∠CEO,∠PED=∠C.則∠PED+∠OED=90°,即∠OEP=90°,然后根據(jù)切線的性質定理可判定PE是⊙O的切線;
(2)利用圓周角定理得到∠AEB=90°,再利用AE∥CD得到∠EFD=90°,接著利用等角的余角相等可判斷∠FED=∠C,所以∠PED=∠FED.
解答 證明:(1)連接OE,如圖,
∵CD為直徑,
∴∠CED=90°,即∠CEO+∠OED=90°,
∵OC=OE,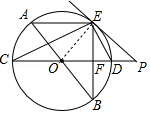
∴∠C=∠CEO,
∴∠C+∠OED=90°,
∵∠PED=∠C.
∴∠PED+∠OED=90°,即∠OEP=90°,
∴OE⊥PE,
∴PE是⊙O的切線;
(2)∵AB為直徑,
∴∠AEB=90°,
而AE∥CD,
∴∠EFD=90°,
∴∠FED+∠EDF=90°,
而∠C+∠EDC=90°,
∴∠FED=∠C,
∴∠PED=∠FED,
∴ED平分∠BEP.
點評 本題考查了切線的性質:經(jīng)過半徑的外端且垂直于這條半徑的直線是圓的切線.當已知條件中明確指出直線與圓有公共點時,常連接過該公共點的半徑,證明該半徑垂直于這條直線.也考查了圓周角定理.


 一線名師提優(yōu)試卷系列答案
一線名師提優(yōu)試卷系列答案科目:初中數(shù)學 來源: 題型:填空題
 2002年國際數(shù)學家大會在中國北京舉行,這是21世紀全世界數(shù)學家的第一次大聚會.這次大會的會徽就是左圖,選定的是我國古代數(shù)學家趙爽用來證明勾股定理的弦圖,可以說是充分肯定了我國數(shù)學的成就,也弘揚了我國古代的數(shù)學文化.弦圖是由四個全等的直角三角形和中間的小正方形拼成的一個大正方形.如果大正方形的面積是13,小正方形的面積是1,直角三角形的較短直角邊長為a,較長直角邊長為b,那么(a+b)2的值是25.
2002年國際數(shù)學家大會在中國北京舉行,這是21世紀全世界數(shù)學家的第一次大聚會.這次大會的會徽就是左圖,選定的是我國古代數(shù)學家趙爽用來證明勾股定理的弦圖,可以說是充分肯定了我國數(shù)學的成就,也弘揚了我國古代的數(shù)學文化.弦圖是由四個全等的直角三角形和中間的小正方形拼成的一個大正方形.如果大正方形的面積是13,小正方形的面積是1,直角三角形的較短直角邊長為a,較長直角邊長為b,那么(a+b)2的值是25.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
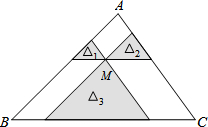 如圖,點M是△ABC內一點,過點M分別作直線平行于△ABC的各邊,所形成的三個小三角形△1,△2,△3(圖中的陰影部分)的面積是4,9,49,則△ABC的面積是( )
如圖,點M是△ABC內一點,過點M分別作直線平行于△ABC的各邊,所形成的三個小三角形△1,△2,△3(圖中的陰影部分)的面積是4,9,49,則△ABC的面積是( )| A. | 62 | B. | 186 | C. | 132 | D. | 144 |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com