
分析 過B作BH⊥x軸于H,如圖,利用旋轉的性質得OB=OA=2$\sqrt{2}$,∠AOB=135°,則∠BOH=45°,所以△OBH為等腰直角三角形,則BH=OH=$\frac{\sqrt{2}}{2}$×2$\sqrt{2}$=2,然后根據第二象限點內點的坐標特征寫出B點坐標.
解答 解:過B作BH⊥x軸于H,如圖,
∵點A的坐標為(2$\sqrt{2}$,0),
∴OA=2$\sqrt{2}$,
∵點A繞著原點按逆時針方向旋轉135°得到點B,
∴OB=OA=2$\sqrt{2}$,∠AOB=135°,
∴∠BOH=45°,
∴△OBH為等腰直角三角形,
∴BH=OH=$\frac{\sqrt{2}}{2}$×2$\sqrt{2}$=2,
∴B(-2,2).
故答案為(-2,2).
點評 本題考查了坐標與圖形變化-旋轉:圖形或點旋轉之后要結合旋轉的角度和圖形的特殊性質來求出旋轉后的點的坐標.常見的是旋轉特殊角度如:30°,45°,60°,90°,180°.


 第1卷單元月考期中期末系列答案
第1卷單元月考期中期末系列答案科目:初中數學 來源: 題型:解答題
 如圖,AB、CD為⊙O的直徑,弦AE∥CD,連接BE交CD于點F,過點E作直線EP與CD的延長線交于點P,使∠PED=∠C.
如圖,AB、CD為⊙O的直徑,弦AE∥CD,連接BE交CD于點F,過點E作直線EP與CD的延長線交于點P,使∠PED=∠C.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
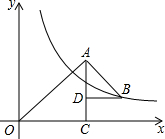 如圖,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函數y=$\frac{6}{x}$在第一象限的圖象經過點B,則△OAC與△BAD的面積之差S△OAC-S△BAD為( )
如圖,△OAC和△BAD都是等腰直角三角形,∠ACO=∠ADB=90°,反比例函數y=$\frac{6}{x}$在第一象限的圖象經過點B,則△OAC與△BAD的面積之差S△OAC-S△BAD為( )| A. | 3 | B. | 6 | C. | 12 | D. | 36 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{2}$ | B. | 2 | C. | -$\frac{1}{2}$ | D. | -2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1個 | B. | 2個 | C. | 3個 | D. | 4個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com