
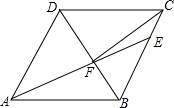
 如圖,在菱形ABCD中,AB=6,∠DAB=60°,點E在BC邊上,且CE=2,AE與BD交于點F,連接CF,則下列結論不正確的是( )
如圖,在菱形ABCD中,AB=6,∠DAB=60°,點E在BC邊上,且CE=2,AE與BD交于點F,連接CF,則下列結論不正確的是( )| A. | △ABF≌△CBF | B. | △ADF∽△EBF | C. | tan∠EAB=$\frac{\sqrt{3}}{3}$ | D. | S△EAB=6$\sqrt{3}$ |
分析 連接AC,過E作EM⊥AB于M,解直角三角形求出EM,根據菱形的性質得出∠ABF=∠CBF,AB=BC,AD∥BC,再逐個判斷即可.
解答 解:A、∵四邊形BACD是菱形,
∴∠ABF=∠CBF,AB=BC,
在△ABF和△CBF中
$\left\{\begin{array}{l}{AB=CB}\\{∠ABF=∠CBF}\\{BF=BF}\end{array}\right.$
∴△ABF≌△CBF,故本選項不符合題意;
B、∵四邊形ABCD是菱形,
∴AD∥BC,
∴△ADF∽△EBF,故本選項不符合題意;
C、連接AC,
∵四邊形BACD是菱形,∠DAB=60°,
∴∠CAB=$\frac{1}{2}$∠DAB=30°,
∴tan∠CAB=tan30°=$\frac{\sqrt{3}}{3}$,
∵∠EAB<tan30°,
∴tan∠EAB=$\frac{\sqrt{3}}{3}$錯誤,故本選項符合題意;
D、
過E作EM⊥AB于M,
∵四邊形ABCD是菱形,AB=6,∠DAB=60°,
∴AB=BC=6,AD∥BC,
∴∠EBM=∠DAB=60°,
∵CE=2,
∴BE=4,
∴EM=BE×sin60°=2$\sqrt{3}$,
∴S△EAB=$\frac{1}{2}×AB×EM$=$\frac{1}{2}$×6×2$\sqrt{3}$=6$\sqrt{3}$,故本選項不符合題意;
故選C.
點評 本題考查了解直角三角形,相似三角形的判定,菱形的性質,全等三角形的判定等知識點,能靈活運用知識點進行推理是解此題的關鍵.


 千里馬走向假期期末仿真試卷寒假系列答案
千里馬走向假期期末仿真試卷寒假系列答案科目:初中數學 來源: 題型:填空題
 如圖,在直角坐標系中,直線l與y軸正半軸所夾的銳角為60°,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1,以A1B、BA為鄰邊作?ABA1C1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2,以A2B1、B1A1為鄰邊作?A1B1A2C2;…;按此作法繼續下去,則C3的坐標是(-16$\sqrt{3}$,64);Cn的坐標是(-22(n-1)$\sqrt{3}$,22n)(n為正整數).
如圖,在直角坐標系中,直線l與y軸正半軸所夾的銳角為60°,過點A(0,1)作y軸的垂線交直線l于點B,過點B作直線l的垂線交y軸于點A1,以A1B、BA為鄰邊作?ABA1C1;過點A1作y軸的垂線交直線l于點B1,過點B1作直線l的垂線交y軸于點A2,以A2B1、B1A1為鄰邊作?A1B1A2C2;…;按此作法繼續下去,則C3的坐標是(-16$\sqrt{3}$,64);Cn的坐標是(-22(n-1)$\sqrt{3}$,22n)(n為正整數).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
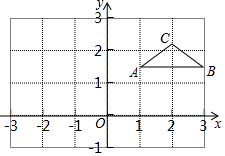 如圖,△ABC在平面直角坐標系內,它的三個頂點的坐標分別為A(1,$\sqrt{2}$),B(3,$\sqrt{2}$),C(2,$\sqrt{5}$),求△ABC的面積.
如圖,△ABC在平面直角坐標系內,它的三個頂點的坐標分別為A(1,$\sqrt{2}$),B(3,$\sqrt{2}$),C(2,$\sqrt{5}$),求△ABC的面積.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 極差是2環 | B. | 中位數是8環 | C. | 眾數是9環 | D. | 平均數是9環 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
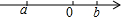 在數軸上實數a,b的位置如圖所示,化簡|a+b|+$\sqrt{(a-b)^{2}}$的結果是( )
在數軸上實數a,b的位置如圖所示,化簡|a+b|+$\sqrt{(a-b)^{2}}$的結果是( )| A. | -2a-b | B. | -2a+b | C. | -2b | D. | -2a |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com