
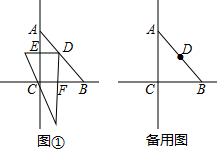
分析 先根據ASA判定△DCE≌△DFB,得出DE=DF,再根據∠EDF=90°,得到△DEF是等腰直角三角形,進而得出∠FEG=45°,再分三種情況進行討論:當G在線段CB延長線上時;當G與B重合時;當G在線段BC上時,分別求得FG的長即可.
解答 解:∵AC=BC,∠C=90°,D為AB中點,連接CD,
∴CD平分∠ACB,CD⊥AB,
∵∠DCB=∠B=45°,
∴CD=DB,
∵∠EDC+∠CDF=∠CDF+∠FDB=90°,
∴∠EDC=∠FDB,
在△DCE和△DFB中,
$\left\{\begin{array}{l}{∠EDC=∠FDB}\\{CD=DB}\\{∠DCE=∠B}\end{array}\right.$,
∴△DCE≌△DFB(ASA),
∴DE=DF,
又∵∠EDF=90°,
∴△DEF是等腰直角三角形,
∴∠FEG=45°,
如圖,當G在線段CB延長線上時,∠FGE<45°,∠EFG>90°,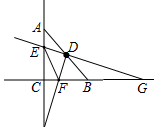
∴EF<GF,
∴△EFG不是等腰三角形;
如圖,當G與B重合時,E與A重合,F與C重合,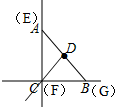
此時FE=AC=2,FG=CB=2,
如圖,當G在線段BC上時,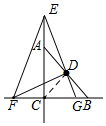
根據∠EGF>45°,∠EFG>45°,∠FEG=45°,可得EF=EG,
∵EC⊥FG,
∴FC=CG,
∵∠EDF=90°,
∴∠FDG=90°,
∴DC=$\frac{1}{2}$FG,即FG=2CD,
又∵等腰Rt△ABC中,CD=$\frac{1}{2}$AB=$\frac{1}{2}$×2$\sqrt{2}$=$\sqrt{2}$,
∴FG=2$\sqrt{2}$.
綜上所述,當△EFG為等腰三角形時,則FG=2或2$\sqrt{2}$.
故答案為:2或2$\sqrt{2}$.
點評 本題主要考查了旋轉的性質,等腰直角三角形的判定以及全等三角形的判定與性質的綜合應用;等腰三角形的頂角平分線、底邊上的中線、底邊上的高相互重合.解決問題的關鍵是判定△DEF是等腰直角三角形,解題時注意分類思想的運用.


科目:初中數學 來源: 題型:解答題
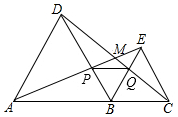 如圖,點A、B、C在一條直線上,△ABD、△BCE均為等邊三角形,連接AE和CD,AE分別交BD、CD于點P、M,CD交BE于點Q,連接PQ.
如圖,點A、B、C在一條直線上,△ABD、△BCE均為等邊三角形,連接AE和CD,AE分別交BD、CD于點P、M,CD交BE于點Q,連接PQ.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,以AB為直徑的⊙O中,CD是弦,CD∥AB,連接AC,BD交于點M.
如圖,以AB為直徑的⊙O中,CD是弦,CD∥AB,連接AC,BD交于點M.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | x(m-x)(n-x) | B. | x2(m-x)(n-x) | C. | $\frac{1}{3}$x(m-2n)(n-2x) | D. | x(m-2x)(n-2x) |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
| 種子個數 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| 發芽種子個數 | 94 | 187 | 282 | 338 | 435 | 530 | 624 | 718 | 814 | 901 |
| 發芽種子頻率 | 0.940 | 0.935 | 0.940 | 0.845 | 0.870 | 0.883 | 0.891 | 0.898 | 0.904 | 0.901 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com