
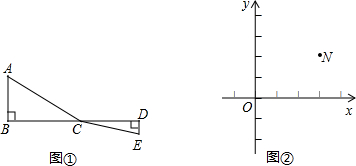
分析 (1)當點C到A、E兩點的距離相等即AC=EC,由勾股定理建立方程,解方程即可;
(2)根據在直線OX上的同側有兩個點M、N,在直線OX上有到M、M的距離之和最短的點存在,可以通過軸對稱來確定,即作出其中一點關于直線OX的對稱點,對稱點與另一點的連線與OX的交點就是所要找的P.再利用勾股定理計算即可.
解答 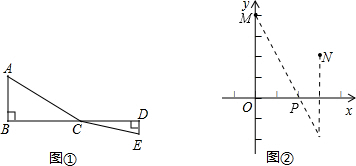 解:(1)∵BC=x,BD=8,
解:(1)∵BC=x,BD=8,
∴CD=8-x,
∵AC=EC,
∴x2+52=(8-x)2+12,
解得:x=$\frac{5}{2}$,
∴當BC=$\frac{5}{2}$時,點C到A、E兩點的距離相等;
(2)如圖所示:P(2,0),
∵PM=$\sqrt{O{P}^{2}+O{M}^{2}}$=$\sqrt{20}$=2$\sqrt{5}$,
PN=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴PM+PN最小值為 3$\sqrt{5}$.
點評 本題利用了數形結合的思想,可通過構造直角三角形,利用勾股定理求解和利用軸對稱求最短路線問題.


 名師伴你成長課時同步學練測系列答案
名師伴你成長課時同步學練測系列答案科目:初中數學 來源: 題型:選擇題
| A. | 3-$2\sqrt{2}$ | B. | 3+$2\sqrt{2}$ | C. | 6-4$\sqrt{2}$ | D. | 6+4$\sqrt{2}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
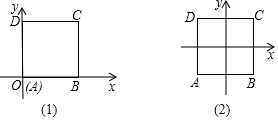 已知正方形ABCD,邊長為1cm.
已知正方形ABCD,邊長為1cm.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
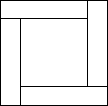 小明同學用四張長為x,寬為y的長方形卡片,拼出如圖所示的包含兩個正方形的圖形(任意兩張相鄰的卡片之間沒有重疊,沒有空隙).
小明同學用四張長為x,寬為y的長方形卡片,拼出如圖所示的包含兩個正方形的圖形(任意兩張相鄰的卡片之間沒有重疊,沒有空隙).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
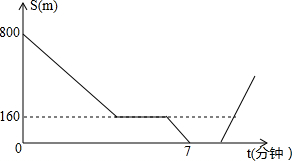 在一次集訓中,一支隊伍出發20分鐘后,通訊員騎自行車追上隊尾傳達命令,然后按原速到隊首傳達命令后維續按原速原路返回,在此過程中隊伍一直保持勻速行進,如圖所示是通訊員與隊首的距離S(米)和通訊員所用時間t(分鐘)之間的函數圖象,若傳達命令所花時間都為2分鐘.則當通訊員再次回到隊尾時.他一共走了$\frac{3880}{3}$米.
在一次集訓中,一支隊伍出發20分鐘后,通訊員騎自行車追上隊尾傳達命令,然后按原速到隊首傳達命令后維續按原速原路返回,在此過程中隊伍一直保持勻速行進,如圖所示是通訊員與隊首的距離S(米)和通訊員所用時間t(分鐘)之間的函數圖象,若傳達命令所花時間都為2分鐘.則當通訊員再次回到隊尾時.他一共走了$\frac{3880}{3}$米.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com