
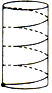
 為籌備元旦晚會,同學們設計了一個圓筒形燈罩,底色漆成白色,然后纏繞紅色油紙,如圖,已知圓筒高108cm,其平行底面的截面周長為36cm,如果在表面纏繞4圈,需要油紙的長度為180cm.
為籌備元旦晚會,同學們設計了一個圓筒形燈罩,底色漆成白色,然后纏繞紅色油紙,如圖,已知圓筒高108cm,其平行底面的截面周長為36cm,如果在表面纏繞4圈,需要油紙的長度為180cm. 分析 將圓柱體沿一條母線展開,可得圖形,如下圖,只需求出每一圈所需的油紙的長度即可,展開后即轉化為求解直角三角形的問題,在Rt△ABC中,AB已知,BC=$\frac{108}{4}$cm,根據勾股定理即可得出AC的長度,由于油紙纏繞4圈,故油紙的總長度為4AC的長度.
解答 解:將圓筒展開后成為一個矩形,如圖,整個油紙也隨之分成相等4段只需求出AC長即可,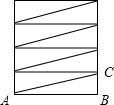 在Rt△ABC中,
在Rt△ABC中,
∵AB=36,BC=$\frac{108}{4}$cm,
∴AC2=AB2+BC2=362+272,
∴AC=45cm,
∴整個油紙的長為45×4=180(cm).
故答案為:180.
點評 本題考查的是平面展開-最短路徑問題,此類問題應先根據題意把立體圖形展開成平面圖形后,再確定兩點之間的最短路徑.一般情況是兩點之間,線段最短.在平面圖形上構造直角三角形解決問題.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
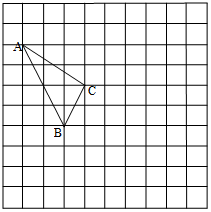 在如圖所示的正方形網格中,每個小正方形的邊長為1,格點三角形(頂點是網格線的交點的三角形)ABC的頂點A、C的坐標分別為(-4,3)、(-1,1).
在如圖所示的正方形網格中,每個小正方形的邊長為1,格點三角形(頂點是網格線的交點的三角形)ABC的頂點A、C的坐標分別為(-4,3)、(-1,1).查看答案和解析>>
科目:初中數學 來源: 題型:填空題
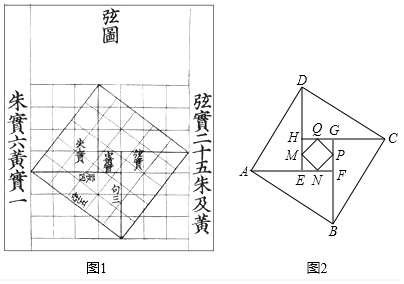
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com