
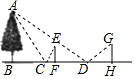
 某一天,小明和小亮來到一河邊,想用平面鏡和皮尺測量這條河的大致寬度,兩人在確保無安全隱患的情況下,現在河岸邊選擇了一點C(點C與河對岸岸邊上的一棵樹的底部點B所確定的直線垂直于河岸).
某一天,小明和小亮來到一河邊,想用平面鏡和皮尺測量這條河的大致寬度,兩人在確保無安全隱患的情況下,現在河岸邊選擇了一點C(點C與河對岸岸邊上的一棵樹的底部點B所確定的直線垂直于河岸).分析 根據題意求出△ABC∽△EFC,△ABD∽△GHD,再根據相似三角形對應邊成比例列式求解即可.
解答  解:由題意可得:∠ACB=∠ECF,∠ADB=∠GDH.
解:由題意可得:∠ACB=∠ECF,∠ADB=∠GDH.
∵AB⊥BH,EF⊥BH,GH⊥BH,
∴∠ABC=∠EFC=∠CHD=90°,
∴△ABC∽△EFC,
∴$\frac{EF}{AB}$=$\frac{CF}{BC}$,即$\frac{1.5}{AB}$=$\frac{1}{BC}$.
∵∠ADB=∠GDH,∠ABC=∠GHD=90°,
∴△ABD∽△GHD,
∴$\frac{GH}{AB}$=$\frac{DH}{BD}$,即$\frac{1.6}{AB}$=$\frac{2}{BC+8.4}$,
解得BC=9.6m.
答:河寬BC是9.6m.
點評 本題考查了相似三角形的應用,讀懂題目信息得到兩三角形相等的角并確定出相似三角形是解題的關鍵,也是本題的難點.


 寒假大串聯黃山書社系列答案
寒假大串聯黃山書社系列答案科目:初中數學 來源: 題型:填空題
 如圖,點A、B在數軸上,其對應的數分別是-14和10,若點C也在這個數軸上,且AC:BC=2:5,則點C對應的數是-$\frac{50}{7}$或-30.
如圖,點A、B在數軸上,其對應的數分別是-14和10,若點C也在這個數軸上,且AC:BC=2:5,則點C對應的數是-$\frac{50}{7}$或-30.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在△ABC中,∠C=90°,AB=10cm,AC=8cm.點P從點C出發沿CB以1cm/s的速度向終點B勻速運動;同時點Q從點A出發沿AB以acm/s的速度向點B勻速運動,以點C為圓心,CP為長為半徑畫⊙C交AC于點D,連接PQ、DQ、PD.若在運動的過程中PQ與⊙C始終保持相切,設運動時間為ts.
如圖,在△ABC中,∠C=90°,AB=10cm,AC=8cm.點P從點C出發沿CB以1cm/s的速度向終點B勻速運動;同時點Q從點A出發沿AB以acm/s的速度向點B勻速運動,以點C為圓心,CP為長為半徑畫⊙C交AC于點D,連接PQ、DQ、PD.若在運動的過程中PQ與⊙C始終保持相切,設運動時間為ts.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,給出的以下四個結論,(1)abc=0,(2)a+b+c>0,(3)a>b,(4)a-b+c>0其中正確的是(1)(4)(填序號).
二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,給出的以下四個結論,(1)abc=0,(2)a+b+c>0,(3)a>b,(4)a-b+c>0其中正確的是(1)(4)(填序號).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com