
 如圖,在△ABC中,∠C=90°,AB=10cm,AC=8cm.點P從點C出發(fā)沿CB以1cm/s的速度向終點B勻速運動;同時點Q從點A出發(fā)沿AB以acm/s的速度向點B勻速運動,以點C為圓心,CP為長為半徑畫⊙C交AC于點D,連接PQ、DQ、PD.若在運動的過程中PQ與⊙C始終保持相切,設(shè)運動時間為ts.
如圖,在△ABC中,∠C=90°,AB=10cm,AC=8cm.點P從點C出發(fā)沿CB以1cm/s的速度向終點B勻速運動;同時點Q從點A出發(fā)沿AB以acm/s的速度向點B勻速運動,以點C為圓心,CP為長為半徑畫⊙C交AC于點D,連接PQ、DQ、PD.若在運動的過程中PQ與⊙C始終保持相切,設(shè)運動時間為ts.分析 (1)如圖1中,作QM⊥AC于M.首先證明四邊形PCMQ是矩形,由QM∥BC,得$\frac{QM}{BC}$=$\frac{AQ}{AB}$,可得方程$\frac{t}{6}$=$\frac{at}{10}$,解方程即可.
(2)由PQ∥AC,得$\frac{PQ}{AC}$=$\frac{BP}{BC}$,即$\frac{PQ}{8}$=$\frac{6-t}{6}$,推出PQ=$\frac{4}{3}$(6-t),根據(jù)S△PQD=$\frac{2}{9}$S△ABC,列出方程,解方程即可.
(3)分兩種情形討論)①當(dāng)∠PDQ=90°,易知△PDQ是等腰直角三角形,則有$\frac{1}{2}$PQ=PC,②當(dāng)∠PQD=90°時,則有AM+CD=8,分別構(gòu)建方程解決問題.
解答 解:(1)如圖1中,作QM⊥AC于M.
在Rt△ABC中,∵AB=10,AC=8,
BC=$\sqrt{1{0}^{2}-{8}^{2}}$=6,
∵PQ是⊙C的切線,
∴PQ⊥BC,
∴∠QPC=∠PCM=∠CMQ=90°,
∴四邊形PCMQ是矩形,
∴QM=PC=t,
∵QM∥BC,
∴$\frac{QM}{BC}$=$\frac{AQ}{AB}$
∴$\frac{t}{6}$=$\frac{at}{10}$,
∴a=$\frac{5}{3}$cm/s.
故答案為$\frac{5}{3}$.
(2)∵PQ∥AC,
∴$\frac{PQ}{AC}$=$\frac{BP}{BC}$,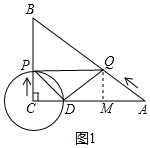
∴$\frac{PQ}{8}$=$\frac{6-t}{6}$,
∴PQ=$\frac{4}{3}$(6-t),
∵S△PQD=$\frac{2}{9}$S△ABC,
∴$\frac{1}{2}$•$\frac{4}{3}$(6-t)•t=$\frac{2}{9}$•$\frac{1}{2}$•6•8,
∴t=2或4.
(3)①當(dāng)∠PDQ=90°,易知△PDQ是等腰直角三角形,則有$\frac{1}{2}$PQ=PC,
∴$\frac{4}{3}$(6-t)=2t,
∴t=$\frac{12}{5}$.
②當(dāng)∠PQD=90°時,則有AM+CD=8,
∴$\frac{4}{3}$t+t=8,
∴t=$\frac{24}{7}$,
綜上所述,t=$\frac{18}{11}$s或$\frac{24}{7}$s時,△PQD是直角三角形.
點評 本題考查圓綜合題、矩形的判定和性質(zhì)、平行線分線段成比例定理、三角形的面積等知識,解題的關(guān)鍵是靈活運用所學(xué)知識,學(xué)會用分類討論的思想思考問題,學(xué)會把問題轉(zhuǎn)化為方程解決,屬于中考壓軸題.


科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 調(diào)查全國初中生的身體素質(zhì)情況 | |
| B. | 調(diào)查一批蠟燭的使用壽命 | |
| C. | 調(diào)查一架“殲20”隱形戰(zhàn)機各部零件的質(zhì)量 | |
| D. | 調(diào)查我國2012年中央電視臺春節(jié)聯(lián)歡晚會的收視率 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | m=1 | B. | m=-1 | C. | m=2 | D. | m無法求出 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 3個 | B. | 4個 | C. | 5個 | D. | 6個 |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
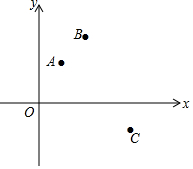 如圖7,在平面直角坐標(biāo)系中,已知某個二次函數(shù)的圖象經(jīng)過點A(1,m),B(2,n),C(4,t),且點B是該二次函數(shù)圖象的頂點.請在圖7中描出該函數(shù)圖象上另外的兩個點,并畫出圖象.
如圖7,在平面直角坐標(biāo)系中,已知某個二次函數(shù)的圖象經(jīng)過點A(1,m),B(2,n),C(4,t),且點B是該二次函數(shù)圖象的頂點.請在圖7中描出該函數(shù)圖象上另外的兩個點,并畫出圖象.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
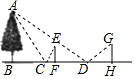 某一天,小明和小亮來到一河邊,想用平面鏡和皮尺測量這條河的大致寬度,兩人在確保無安全隱患的情況下,現(xiàn)在河岸邊選擇了一點C(點C與河對岸岸邊上的一棵樹的底部點B所確定的直線垂直于河岸).
某一天,小明和小亮來到一河邊,想用平面鏡和皮尺測量這條河的大致寬度,兩人在確保無安全隱患的情況下,現(xiàn)在河岸邊選擇了一點C(點C與河對岸岸邊上的一棵樹的底部點B所確定的直線垂直于河岸).查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com