
分析 (1)設每臺空調的進價為m元,則每臺電冰箱的進價為(m+400)元,根據(jù)數(shù)量=總價÷單價結合80000元購進電冰箱的數(shù)量與用64000元購進空調的數(shù)量相等即可得出關于m的分式方程,解之即可得出結論;
(2)設購進電冰箱x臺(x為正整數(shù)),這100臺家電的銷售總利潤為y元,根據(jù)總利潤=電冰箱的總利潤+空調總利潤即可得出y關于x的函數(shù)關系式,結合“購進空調數(shù)量不超過電冰箱數(shù)量的2倍,總利潤不低于13200元”即可得出關于x的一元一次不等式組,解之即可得出x的取值范圍,取其內的正整數(shù)即可得出所有購買方案,再根據(jù)一次函數(shù)的性質即可解決最值問題.
解答 解:(1)設每臺空調的進價為m元,則每臺電冰箱的進價為(m+400)元,
根據(jù)題意得:$\frac{80000}{m+400}$=$\frac{64000}{m}$,
解得:m=1600,
經檢驗,m=1600是原方程的解,
∴m+400=1600+400=2000.
答:每臺空調的進價為1600元,每臺電冰箱的進價為2000元.
(2)設購進電冰箱x臺(x為正整數(shù)),這100臺家電的銷售總利潤為y元,
則y=(2100-2000)x+(1750-1600)(100-x)=-50x+15000,
根據(jù)題意得:$\left\{\begin{array}{l}{100-x≤2x}\\{-50x+15000≥13200}\end{array}\right.$,
解得:33$\frac{1}{3}$≤x≤36,
∵x為正整數(shù),
∴x=34,35,36,
∴合理的方案共有3種,
即①電冰箱34臺,空調66臺;
②電冰箱35臺,空調65臺;
③電冰箱36臺,空調64臺;
∵y=-50x+15000,k=-50<0,
∴y隨x的增大而減小,
∴當x=34時,y有最大值,最大值為:-50×34+15000=13300(元),
答:當購進電冰箱34臺,空調66臺獲利最大,最大利潤為13300元.
點評 本題考查了分式方程的應用、一次函數(shù)的性質以及解一元一次不等式組,解題的關鍵是:(1)根據(jù)數(shù)量=總價÷單價列出關于m的分式方程;(2)根據(jù)總利潤=電冰箱的總利潤+空調總利潤找出y關于x的函數(shù)關系式.


科目:初中數(shù)學 來源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | -$\frac{1}{3}$x-5=4,得$\frac{1}{3}$x=4+5 | B. | 5y-3y+y=9,得(5-3)y=9 | ||
| C. | x+7=26,得x=19 | D. | -5x=20,得x=-$\frac{5}{20}$ |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
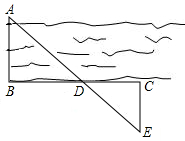 如圖,為了估算河的寬度,我們可以在河對岸選定一個目標作為點A,再在河的這一邊選點B和C,使AB⊥BC,然后再選點E,使EC⊥BC,用視線確定BC和AE的交點D,此時如果測得BD=150米,DC=60米,EC=50米,試求兩岸間的距離AB.
如圖,為了估算河的寬度,我們可以在河對岸選定一個目標作為點A,再在河的這一邊選點B和C,使AB⊥BC,然后再選點E,使EC⊥BC,用視線確定BC和AE的交點D,此時如果測得BD=150米,DC=60米,EC=50米,試求兩岸間的距離AB.查看答案和解析>>
湖北省互聯(lián)網違法和不良信息舉報平臺 | 網上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com