
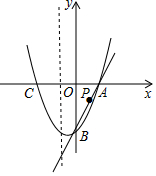
 如圖,直線y=3x-6與x軸相交于點A,與y軸相交于點B,拋物線y=x2+bx+c過點A、B兩點,該拋物線與x軸的另一個交點為C.
如圖,直線y=3x-6與x軸相交于點A,與y軸相交于點B,拋物線y=x2+bx+c過點A、B兩點,該拋物線與x軸的另一個交點為C.分析 (1)分別令直線y=3x-6中,x和y分別為0可求得對應的y和x的值,故此可得到點A和點B的坐標,然后將點A和點B的坐標代入拋物線的解析式可得到關(guān)于b、c的方程,從而可求得b,c的值,故此可得到拋物線的解析式;
(2)過點P作PD⊥AC,垂足為D,依據(jù)平行線的分線段成比例定理可求得OD的長,從而得到點P的橫坐標,然后將點P的橫坐標代入直線AB的解析式,可求得點P的縱坐標;
(3)令y=0得:x2+x-6=0,可求得點C的坐標,從而得到AC=5.①當AC為平行四邊形的邊長時,則MN=AC=5.可得到點M的橫縱坐標,然后將點M的橫坐標代入拋物線的解析式可得到點M的縱坐標;②當AC為平行四邊形的對角線時.設(shè)點M的橫坐標為x.依據(jù)中點坐標公式可求得x=-1,將x=-1代入拋物線的解析式得:y=-6.故此可求得此時點M的坐標.
解答 解:(1)令直線y=3x-6中,x=0,則y=-6,
∴B(0,-6).
令直線y=3x-6中,y=0,解得x=2,
∴A(2,0).
將點A和點B的坐標代入拋物線的解析式得:$\left\{\begin{array}{l}{c=-6}\\{4+2b+c=0}\end{array}\right.$,
解得:c=-6,b=1.
∴拋物線的解析式為y=x2+x-6.
(2)如圖1所示:過點P作PD⊥AC,垂足為D.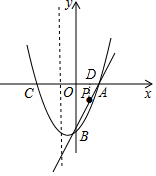
∵PD∥OB,AP:BP=1:2,
∴AD:OD=1:2.
又∵AO=2.
∴OD=$\frac{4}{3}$.
將x=$\frac{4}{3}$代入y=3x-6得:y=-2.
∴點P的坐標為($\frac{4}{3}$,-2).
(3)令y=0得:x2+x-6=0,解得:x=-3或x=2,
∴C(-3,0).
∴AC=5.
①當AC為平行四邊形的邊長時,則MN=AC=5.
又∵點N在y軸上,
∴M的橫坐標為±5.
當M的橫坐標為5時,y=52+5-6=24,
∴M的坐標為(5,24).
當M的橫坐標為-5時,y=(-5)2-5-6=14,
∴M的坐標為(-5,14).
②當AC為平行四邊形的對角線時.設(shè)點M的橫坐標為x.
依據(jù)中點坐標公式可知$\frac{x+0}{2}$=$\frac{-3+2}{2}$,解得x=-1,
將x=-1代入拋物線的解析式得:y=-6.
∴M的坐標為(-1,-6).
綜上所述,點M的坐標為(-1,-6)或(5,24)或(-5,14).
點評 本題主要考查的是二次函數(shù)的綜合應用,解答本題主要應用了待定系數(shù)法求二次函數(shù)的解析式,平行線分線段成比例定理,平行四邊形的性質(zhì),分類討論是解題的關(guān)鍵.


科目:初中數(shù)學 來源: 題型:選擇題
| A. | 過一點有無數(shù)條直線 | B. | 兩點確定一條直線 | ||
| C. | 兩點之間線段最短 | D. | 線段是直線的一部分 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | 平均數(shù) | B. | 眾數(shù) | C. | 中位數(shù) | D. | 方差 |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
| 回收廢舊報紙的質(zhì)量/千克 | 1.5 | 2 | 3.5 | 4 | … |
| 付款全額/元 | 0.75 | 1.0 | 1.9 | 2.2 | … |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源:2017屆浙江省九年級3月模擬數(shù)學試卷(解析版) 題型:填空題
若關(guān)于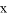 的代數(shù)式的取值范圍是x≤2,則這個代數(shù)式可以為____________(寫出一個即可);
的代數(shù)式的取值范圍是x≤2,則這個代數(shù)式可以為____________(寫出一個即可);
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com