
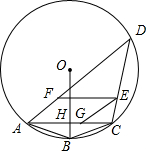
 ⊙O是四邊形ABCD的外接圓.OB⊥AC.OB與AC相交于點H,BC=2$\sqrt{10}$,AC=CD=12
⊙O是四邊形ABCD的外接圓.OB⊥AC.OB與AC相交于點H,BC=2$\sqrt{10}$,AC=CD=12分析 (1)先根據垂徑定理得出直角三角形,進而求出BH,最后用勾股定理即可求出OA;
(2)利用勾股定理先求出OM進而求出AM即可AD的長,
(3)先判斷出四邊形AGEF是平行四邊形,再用三角函數表示出AF和EN,最后用面積公式即可.
解答 解:(1)如圖1, 連接OA,
連接OA,
∵OB⊥AC,
∴AH=CH=$\frac{1}{2}$AC=6,AB=BC=2$\sqrt{10}$,
根據勾股定理得,BH=$\sqrt{A{B}^{2}-A{H}^{2}}$=2,
在Rt△AOH中,OA2-OH2=AH2,
∴OA2-(OA-2)2=36,
∴OA=10,
∴⊙O的半徑為10;
(2)如圖2,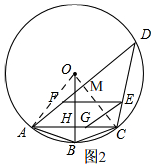 連接OC,OA,
連接OC,OA,
∵AC=CD,
∴OC⊥AD,
∴AD=2AM,
在RtOAM中,AM2=OA2-OM2=100-OM2,
在Rt△ACM中,AM2=AC2-CM2=AC2-(OA-OM)2=144-(10-OM)2=44+20OM-OM2,
∴100-OM2=44+20OM-OM2,
∴OM=$\frac{14}{5}$,
∴AD=2AM=2$\sqrt{1{0}^{2}-(\frac{14}{5})^{2}}$=2×$\frac{48}{5}$=$\frac{96}{5}$,
(3)存在面積最大值,
理由:如圖2中,在Rt△ACM中,CM=10-$\frac{14}{5}$=$\frac{36}{5}$,AC=12,
∴sin∠CAD=$\frac{CM}{AC}$=$\frac{3}{5}$,
設CG=x,(0<x<12)
∴AG=12-x,
∵EG∥AD,
∴$\frac{EG}{AD}=\frac{CG}{AC}$,
∴$\frac{EG}{\frac{96}{5}}=\frac{x}{12}$,
∴EG=$\frac{8}{5}$x,
∵EF∥AC,EG∥AD,
∴四邊形AFEG是平行四邊形,
∴AF=EG=$\frac{8}{5}$x,EF=AG=12-x,
∵EF∥AC,
∴∠NFE=∠CAD,
如圖3,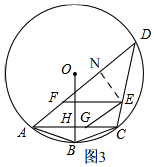 過點E作EN⊥AD,
過點E作EN⊥AD,
∴sin∠NFE=$\frac{EN}{EF}$=$\frac{EN}{12-x}=\frac{3}{5}$,
∴EN=$\frac{3}{5}$(12-x),
∴S四邊形AGEF=AF×EN=$\frac{8}{5}$x•$\frac{3}{5}$(12-x)=-$\frac{24}{25}$(x-6)2+$\frac{864}{25}$,
當x=6時,S四邊形AGEF最大=$\frac{864}{25}$.
點評 此題是圓的綜合題,主要考查了勾股定理,銳角三角函數,平行四邊形的判定和性質,垂徑定理,平行線分線段成比例定理,解本題的關鍵是求出求出圓的半徑,是一道中等難度的中考常考題.


 習題精選系列答案
習題精選系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 3n-1 | B. | 3n+1 | C. | 4n-1 | D. | 4n+1 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
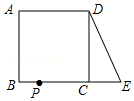 如圖,在正方形ABCD中,AB=2,延長BC到點E,使CE=1,連接DE,動點P從點A出發以每秒1個單位的速度沿AB→BC→CD→DA向終點A運動,設點P的運動時間為t秒,當△ABP和△DCE全等時,t的值為3s或7s.
如圖,在正方形ABCD中,AB=2,延長BC到點E,使CE=1,連接DE,動點P從點A出發以每秒1個單位的速度沿AB→BC→CD→DA向終點A運動,設點P的運動時間為t秒,當△ABP和△DCE全等時,t的值為3s或7s.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 某中學舉行“班班有歌聲”活動,比賽時聘請了10位老師和10位學生擔任評委,其中甲班的得分情況如下統計圖(表)所示.
某中學舉行“班班有歌聲”活動,比賽時聘請了10位老師和10位學生擔任評委,其中甲班的得分情況如下統計圖(表)所示.| 評委序號 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 分數 | 94 | 96 | 93 | 91 | x | 92 | 91 | 98 | 96 | 93 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com