
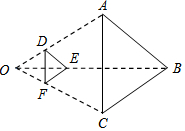
 如圖,以點O為位似中心,將△ABC縮小后得到△DEF,已知OD=1,OA=3.若△DEF的面積為S,則△ABC的面積為( )
如圖,以點O為位似中心,將△ABC縮小后得到△DEF,已知OD=1,OA=3.若△DEF的面積為S,則△ABC的面積為( )| A. | 2S | B. | 3S | C. | 4S | D. | 9S |
分析 利用位似的性質和相似三角形的性質得到$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{OD}{OA}$)2,然后利用比例性質可求出△ABC的面積.
解答 解:∵△ABC與△DEF位似,
∴$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{OD}{OA}$)2=$\frac{1}{9}$,
∴△ABC的面積=9S.
故選D.
點評 本題考查了位似變換:如果兩個圖形不僅是相似圖形,而且對應頂點的連線相交于一點,對應邊互相平行,那么這樣的兩個圖形叫做位似圖形,這個點叫做位似中心.注意:①兩個圖形必須是相似形;②對應點的連線都經過同一點;③對應邊平行.


 中考解讀考點精練系列答案
中考解讀考點精練系列答案科目:初中數學 來源: 題型:解答題
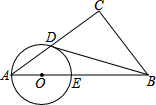 已知:如圖所示,在Rt△ABC中,∠C=90°,點O在AB上,以O為圓心,OA長為半徑的圓與AC,AB分別交于點D,E,且∠CBD=∠A,求證:BD與⊙O相切.
已知:如圖所示,在Rt△ABC中,∠C=90°,點O在AB上,以O為圓心,OA長為半徑的圓與AC,AB分別交于點D,E,且∠CBD=∠A,求證:BD與⊙O相切.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
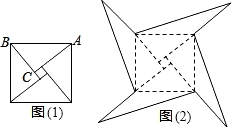 如圖1是我國古代著名的“趙爽弦圖”的示意圖,它是由四個全等的直角三角形圍成的.若AC=6,BC=5,將四個直角三角形中邊長為6的直角邊分別向外延長一倍,得到如圖2所示的“數學風車”,則這個風車的外圍周長是( )
如圖1是我國古代著名的“趙爽弦圖”的示意圖,它是由四個全等的直角三角形圍成的.若AC=6,BC=5,將四個直角三角形中邊長為6的直角邊分別向外延長一倍,得到如圖2所示的“數學風車”,則這個風車的外圍周長是( )| A. | 36 | B. | 76 | C. | 66 | D. | 12 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
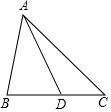 如圖,△ABC中,點D在線段BC上,且△ABC∽△DBA,則下列結論一定正確的是( )
如圖,△ABC中,點D在線段BC上,且△ABC∽△DBA,則下列結論一定正確的是( )| A. | AB2=BC•BD | B. | AB2=AC•BD | C. | AB•AD=BD•BC | D. | AB•AC=BC•BD |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,某輪船在海上以每小時30海里的速度向正西方向航行,上午8:00在點B處測得小島A在北偏東30°方向,上午9:00船到達C處,測得島A在北偏東45°方向,如果輪船繼續向西航行,上午11:00到達點D處,求點D與小島A的距離(精確到0.1海里)
如圖,某輪船在海上以每小時30海里的速度向正西方向航行,上午8:00在點B處測得小島A在北偏東30°方向,上午9:00船到達C處,測得島A在北偏東45°方向,如果輪船繼續向西航行,上午11:00到達點D處,求點D與小島A的距離(精確到0.1海里)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
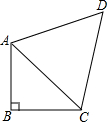 如圖,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.
如圖,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com