
 如圖,某輪船在海上以每小時30海里的速度向正西方向航行,上午8:00在點B處測得小島A在北偏東30°方向,上午9:00船到達C處,測得島A在北偏東45°方向,如果輪船繼續向西航行,上午11:00到達點D處,求點D與小島A的距離(精確到0.1海里)
如圖,某輪船在海上以每小時30海里的速度向正西方向航行,上午8:00在點B處測得小島A在北偏東30°方向,上午9:00船到達C處,測得島A在北偏東45°方向,如果輪船繼續向西航行,上午11:00到達點D處,求點D與小島A的距離(精確到0.1海里) 分析 作AE⊥BC交DC的延長線與E,設AE=x海里,根據正切的定義求出BE,根據直角三角形的性質列出方程,解方程即可.
解答 解: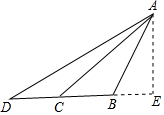 作AE⊥BC交DC的延長線與E,
作AE⊥BC交DC的延長線與E,
設AE=x海里,
則BE=AE•tan30°=$\frac{\sqrt{3}}{3}$x,
∵∠ACE=45°,
∴CE=AE=x,
∴30+$\frac{\sqrt{3}}{3}$x=x,
解得,x=45+15$\sqrt{3}$,
則DE=DC+BC+BE=105+15$\sqrt{3}$,
由勾股定理得,DA=$\sqrt{(105+15\sqrt{3})^{2}+(45+15\sqrt{3})^{2}}$≈149.0海里,
答:點D與小島A的距離約為149.0海里.
點評 本題考查的是解直角三角形的應用-方向角問題,正確標注方向角、熟記銳角三角函數的定義是解題的關鍵.


科目:初中數學 來源: 題型:填空題
 如圖,四邊形ABCD中,點M、N分別在AB,BC上,將△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,∠A=100°,∠C=70°,則∠B=95°.
如圖,四邊形ABCD中,點M、N分別在AB,BC上,將△BMN沿MN翻折,得△FMN,若MF∥AD,FN∥DC,∠A=100°,∠C=70°,則∠B=95°.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
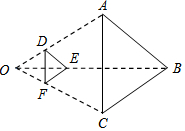 如圖,以點O為位似中心,將△ABC縮小后得到△DEF,已知OD=1,OA=3.若△DEF的面積為S,則△ABC的面積為( )
如圖,以點O為位似中心,將△ABC縮小后得到△DEF,已知OD=1,OA=3.若△DEF的面積為S,則△ABC的面積為( )| A. | 2S | B. | 3S | C. | 4S | D. | 9S |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
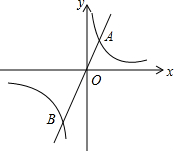 如圖,過原點O的直線與雙曲線y=$\frac{1}{x}$(x>0)交于點A,與雙曲線y=$\frac{k}{x}$(x<0)交于點B.若OB=2OA,則k=4.
如圖,過原點O的直線與雙曲線y=$\frac{1}{x}$(x>0)交于點A,與雙曲線y=$\frac{k}{x}$(x<0)交于點B.若OB=2OA,則k=4.查看答案和解析>>
科目:初中數學 來源: 題型:填空題
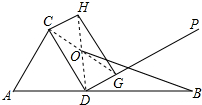 如圖,線段AB的長為10cm,點D在AB上,△ACD為等邊三角形,過點D作DP⊥CD,點G是DP上不與點D重合的一動點,作矩形CDGH.記矩形CDGH的對角線交點為O,連接OA、OB,
如圖,線段AB的長為10cm,點D在AB上,△ACD為等邊三角形,過點D作DP⊥CD,點G是DP上不與點D重合的一動點,作矩形CDGH.記矩形CDGH的對角線交點為O,連接OA、OB,查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在四邊形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
如圖,在四邊形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com