
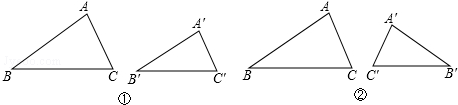
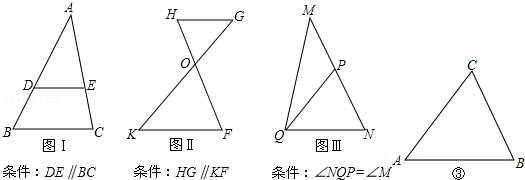
分析 (1)根據互為順相似和互為逆相似的定義即可作出判斷;
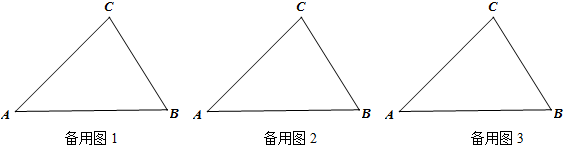
(2)根據點P在△ABC邊上的位置分為三種情況,需要分類討論,逐一分析求解即可.
解答 解:(1)互為順相似的是 ①②;互為逆相似的是 ③;
故答案為:①②,③;
(2)根據點P在△ABC邊上的位置分為以下三種情況:
第一種情況:如圖①,點P在BC(不含點B、C)上,過點P只能畫出2條截線PQ1、PQ2,分別使∠CPQ1=∠A,∠BPQ2=∠A,此時△PQ1C、△PBQ2都與△ABC互為逆相似.
第二種情況:如圖②,點P在AC(不含點A、C)上,過點B作∠CBM=∠A,BM交AC于點M.
當點P在AM(不含點M)上時,過點P1只能畫出1條截線P1Q,使∠AP1Q=∠ABC,此時△AP1Q與△ABC互為逆相似;
當點P在CM上時,過點P2只能畫出2條截線P2Q1、P2Q2,分別使∠AP2Q1=∠ABC,∠CP2Q2=∠ABC,此時△AP2Q1、△Q2P2C都與△ABC互為逆相似.
第三種情況:如圖③,點P在AB(不含點A、B)上,過點C作∠BCD=∠A,∠ACE=∠B,CD、CE分別交AB于點D、E.
當點P在AD(不含點D)上時,過點P只能畫出1條截線P1Q,使∠AP1Q=∠ACB,此時△AQP1與△ABC互為逆相似;
當點P在DE上時,過點P2只能畫出2條截線P2Q1、P2Q2,分別使∠AP2Q1=∠ACB,∠BP2Q2=∠BCA,此時△AQ1P2、△Q2BP2
都與△ABC互為逆相似;
當點P在BE(不含點E)上時,過點P3只能畫出1條截線P3Q′,使∠BP3Q′=∠BCA,此時△Q′BP3與△ABC互為逆相似.
點評 本題是創新型中考壓軸題,主要考查了相似三角形的知識點、分類討論的數學思想以及接受與理解新生事物的能力.準確理解題設條件中“順相似”“逆相似”的定義是正確解題的先決條件,在分析與解決問題的過程中,要考慮全面,進行分類討論,避免漏解.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,在△ABC中,∠ACB=90°,AC=BC,E為AC邊的中點,過點A作AD⊥AB交BE的延長線于點D,CG平分∠ACB交BD于點G,F為AB邊上一點,連接CF,且∠ACF=∠CBG.求證:
如圖,在△ABC中,∠ACB=90°,AC=BC,E為AC邊的中點,過點A作AD⊥AB交BE的延長線于點D,CG平分∠ACB交BD于點G,F為AB邊上一點,連接CF,且∠ACF=∠CBG.求證:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
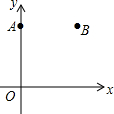 如圖,在平面直角坐標系xOy中,已知點A(0,6),點B(6,6).
如圖,在平面直角坐標系xOy中,已知點A(0,6),點B(6,6).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
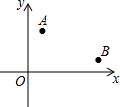 如圖,在平面直角坐標系xOy中,點A(1,3),點B(5,1).
如圖,在平面直角坐標系xOy中,點A(1,3),點B(5,1).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com