Question

1．若將平行四邊形紙片ABCD按如圖1所示方式折疊，使點C與A重合，點D落到D′處，折痕為EF．這時很容易證得：△AEF是等腰三角形．
（1）若將矩形紙片ABCD按上述方式折疊，如圖2．試探究：重疊部分△AEF如果恰好是等邊三角形，這時矩形ABCD的長、寬之比應是多少？證明你的結論；
（2）如圖3，沿EF折疊矩形ABCD，使B點落在AD邊上的B′處；沿B′G折疊，使D點落在D′處，且B′D′過F點． 四邊形B′EFG是什么特殊四邊形？證明你的結論．
（3）在圖3中連接BB′，試判斷并證明△BB′G的形狀．

Answer 1

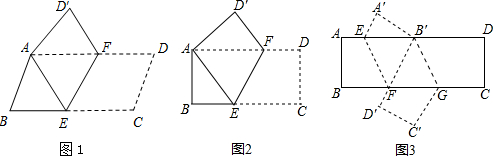
分析 （1）矩形ABCD的長、寬之比應是$\sqrt{3}$．設BE=a，根據等邊三角形的性質可得出∠EAF=60°，根據矩形的性質可得出∠BAD=∠ABE=90°，∠BAE=30°，再根據特殊角的三角函數值即可得出AE=2a，AB=$\sqrt{3}$a，結合邊與邊之間的關系即可得出$\frac{BC}{AB}$=$\sqrt{3}$；
（2）四邊形B′EFG是平行四邊形．根據矩形的性質可得出AD∥BC，從而得出相等的內錯角“∠B′EF=∠BFE，∠EB′F=∠GFB′，∠DB′G=∠FGB”，再由翻折的性質可得出∠BFE=∠B′FE，∠DB′G=∠FB′G，由此即可得出∠B′FE=∠FB′G，從而找出B′E∥FG，由兩組對邊互相平行即可證出四邊形B′EFG是平行四邊形；
（3）△BB′G為直角三角形．連接BB′交EF于點M，根據平行線的性質可得出∠EB′B=∠FBB′，由翻折的性質可得出BF=B′F，從而可得出∠EB′B=∠FB′B，再由等腰三角形的性質可得出∠BMF=90°，根據平行線的性質即可得出∠BB′G=∠BMF=90°，由此即可證出△BB′G為直角三角形．

解答 解：（1）矩形ABCD的長、寬之比應是$\sqrt{3}$．
證明：設BE=a，
∵△AEF等邊三角形，
∴∠EAF=60°，
∵四邊形ABCD為矩形，
∴∠BAD=∠ABE=90°，∠BAE=∠BAD-∠EAF=30°．
在Rt△ABE中，∠ABE=90°，∠BAE=30°，BE=a，
∴AE=$\frac{BE}{sin∠BAE}$=2a，AB=$\frac{BE}{tan∠BAE}$=$\sqrt{3}$a，
∵AE=EC，
∴BC=BE+EC=3a，
∴$\frac{BC}{AB}$=$\frac{3a}{\sqrt{3}a}$=$\sqrt{3}$．
（2）四邊形B′EFG是平行四邊形．
證明：∵四邊形ABCD為矩形，
∴AD∥BC，
∴∠B′EF=∠BFE，∠EB′F=∠GFB′，∠DB′G=∠FGB′．
由翻折的特性可知：∠BFE=∠B′FE，∠DB′G=∠FB′G，
∴∠B′EF=∠B′FE，∠FB′G=∠FGB′，
又∵∠EB′F=∠GFB′，
∴∠B′FE=∠FB′G，
∴EF∥B′G，
又∵B′E∥FG，
∴四邊形B′EFG是平行四邊形．
（3）△BB′G為直角三角形．
證明：連接BB′交EF于點M，如圖所示．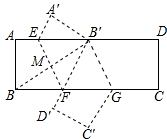

∵AD∥BC，
∴∠EB′B=∠FBB′，
∵BF=B′F，
∴∠FBB′=∠FB′B，
∴∠EB′B=∠FB′B．
∵∠B′EF=∠B′FE，
∴△B′EF為等腰三角形，
∴B′M⊥EF，
∴∠BMF=90°．
∵EF∥B′G，
∴∠BB′G=∠BMF=90°，
∴△BB′G為直角三角形．

點評 本題考查了翻折變換、平行線的性質、平行四邊形的判定定理、特殊角的三角函數值、矩形的性質以及等腰三角形的性質，解題的關鍵是：（1）求出$\frac{BC}{AB}$的值；（2）證出EF∥B′G；（3）證出∠BB′G=∠BMF=90°．本題屬于中檔題，難度不大，解決該題型題目時，根據平行線的性質找出相等的角是關鍵．