
分析 分三種情討論即可①如圖1中,當AE=AF,EF=2$\sqrt{2}$時.②如圖2中,當AE=AF,EF=2$\sqrt{2}$時.③如圖3中,當FA=EF,AE=2$\sqrt{2}$時.
解答 解:①如圖1中,當AE=AF,EF=2$\sqrt{2}$時,易知AE=AF=2.
②如圖2中,當AE=AF,EF=2$\sqrt{2}$時,CE=CF=2,BE=DF=1,AE=AF=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$.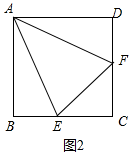
③如圖3中,當FA=EF,AE=2$\sqrt{2}$時,作FG⊥AE于G,則四邊形AGFD是矩形,AD=FG=3,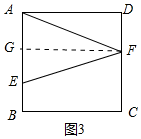
∵FA=FE,FG⊥AE,
∴AG=$\sqrt{2}$,
在Rt△AFG中,AF=EF=$\sqrt{(\sqrt{2})^{2}+{3}^{2}}$=$\sqrt{11}$,
綜上所述,腰三角形AEF的腰長是2或$\sqrt{10}$或$\sqrt{11}$.
故答案為2或$\sqrt{10}$或$\sqrt{11}$.
點評 本題考查正方形的性質、等腰三角形的判定和性質、勾股定理等知識,解題的關鍵是學會用分類討論的思想思考問題,屬于中考常考題型.


科目:初中數學 來源: 題型:解答題
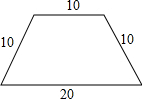 有一根圍成梯形的籬笆,它的各邊長如圖所示,為了其他用處,將它改圍成一個長方形籬笆,使得圍成的長方形的一邊長為10,則此時籬笆圍成的長方形的另一邊長為多少?若改圍成一個正方形的籬笆,正方形的邊長為多少?并比較圍出的長方形和正方形哪個面積更大?
有一根圍成梯形的籬笆,它的各邊長如圖所示,為了其他用處,將它改圍成一個長方形籬笆,使得圍成的長方形的一邊長為10,則此時籬笆圍成的長方形的另一邊長為多少?若改圍成一個正方形的籬笆,正方形的邊長為多少?并比較圍出的長方形和正方形哪個面積更大?查看答案和解析>>
科目:初中數學 來源: 題型:解答題
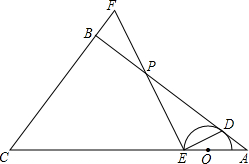 如圖,在△ABC中,∠ABC=90°,AB=4,BC=3,O是邊AC上的一個動點,以點O為圓心作半圓,與邊AB相切于點D,交線段OC于點E,連接ED,過點E作ED的高,交射線AB于點P,交射線CB于點F.
如圖,在△ABC中,∠ABC=90°,AB=4,BC=3,O是邊AC上的一個動點,以點O為圓心作半圓,與邊AB相切于點D,交線段OC于點E,連接ED,過點E作ED的高,交射線AB于點P,交射線CB于點F.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com