
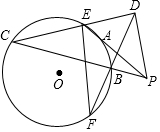
 PA為⊙O的切線,PBC是⊙O的割線,PD=PA,連接CD,BD分別交⊙O于E,F,求證:EF∥PD.
PA為⊙O的切線,PBC是⊙O的割線,PD=PA,連接CD,BD分別交⊙O于E,F,求證:EF∥PD. 分析 根據切割線定理得到PA2=PB•PC,等量代換得到PD2=PB•PC,推出△PBD∽△PDC,根據相似三角形的性質得到∠PDB=∠C,由圓周角定理得到∠C=∠F,等量代換得到∠F=∠PDB,根據平行線的判定即刻得到結論.
解答 證明:∵PA為⊙O的切線,PBC是⊙O的割線,
∴PA2=PB•PC,
∵PD=PA,
∴PD2=PB•PC,
∴$\frac{PD}{PB}$=$\frac{PC}{PD}$,
∵∠DPC=∠BPD,
∴△PBD∽△PDC,
∴∠PDB=∠C,
∵∠C=∠F,
∴∠F=∠PDB,
∴EF∥PD.
點評 本題考查了切線的性質,切割線定理,相似三角形的判定和性質,平行線的判定,熟記掌握切割線定理是解題的關鍵.


科目:初中數學 來源: 題型:選擇題
| A. | y=80x-100 | B. | y=-80x-100 | C. | y=80x+100 | D. | y=-80x+100 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,C為半圓弧O的中點,點P為直徑BA延長線上一點,過點P作半圓的切線PD,D為切點,∠DPB的平分線分別交AC,BC于點E,F; 證明:∠PDA=∠CDF.
如圖,C為半圓弧O的中點,點P為直徑BA延長線上一點,過點P作半圓的切線PD,D為切點,∠DPB的平分線分別交AC,BC于點E,F; 證明:∠PDA=∠CDF.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com