Question

16．如圖1所示，將兩塊全等的直角三角形紙片△ABC和△DEF疊放在一起，其中∠ACB=∠E=90°，BC=DE=6，AC=FE=8，頂點D在邊AB上．

（1）若DE經過點C，且AD=CD=BD，DF交AC于點G，求重疊部分（△DCG）的面積；
（2）思考探究：“數學學習小組”的幾位同學受到啟發，保持（1）中的點D不動，將△DEF繞點D旋轉，使DE⊥AB交AC于點H，DF交AC于點G，如圖2，求△ADH的面積．

Answer 1

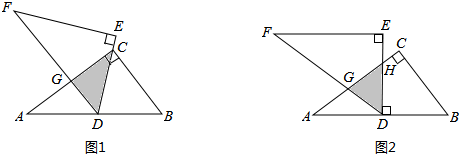
分析 （1）先求出∠B=∠DCB，再證明DG∥BC，然后證出DG⊥AC，G是AC的中點，即可求出重疊部分（△DCG）的面積；
（2）先證明AG=GH，再求出AD，然后證明△ADH∽△ACB，得出比例式$\frac{AD}{AC}$=$\frac{DH}{CB}$，求出DH，即可求出△ADH的面積．

解答 解：（1）∵∠ACB=90°，D是AB的中點，
∴DC=DB=DA，
∴∠B=∠DCB，
又∵△ABC≌△FDE，
∴∠FDE=∠B，
∴∠FDE=∠DCB，
∴DG∥BC，
∴∠AGD=∠ACB=90°，
∴DG⊥AC，
又∵DC=DA，
∴G是AC的中點，
∴CG=$\frac{1}{2}$AC=$\frac{1}{2}$×8=4，DG=$\frac{1}{2}$BC=$\frac{1}{2}$×6=3，
∴S_△DCG=$\frac{1}{2}$×CG×DG=$\frac{1}{2}$×4×3=6．

（2）如圖2，∵△ABC≌△FDE，
∴∠B=∠1，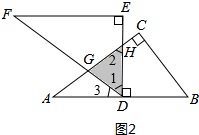
∵∠C=90°，ED⊥AB，
∴∠A+∠B=90°，∠A+∠2=90°，
∴∠B=∠2，
∴∠1=∠2，
∴GH=GD，
∵∠A+∠2=90°，∠1+∠3=90°，
∴∠A=∠3，
∴AG=GD，
∴AG=GH，
∴點G為AH的中點，
在Rt△ABC中，AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{8}^{2}+{6}^{2}}$=10，
∵D是AB中點，
∴AD=$\frac{1}{2}$AB=5，
在△ADH與△ACB中，
∵∠A=∠A，∠ADH=∠ACB=90°，
∴△ADH∽△ACB，
∴$\frac{AD}{AC}$=$\frac{DH}{CB}$，即$\frac{5}{8}$=$\frac{DH}{6}$，
∴DH=$\frac{15}{4}$，
∴S_△ADH=$\frac{1}{2}$×DH×AD=$\frac{1}{2}$×$\frac{15}{4}$×5=$\frac{75}{8}$．

點評 本題考查了全等三角形的性質、直角三角形斜邊上的中線性質以及勾股定理和三角形面積的計算的綜合應用；解決問題的關鍵是根據相似三角形的對應邊成比例，列出比例式進行求解．