
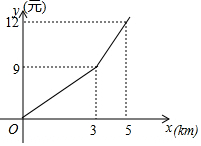
 某出租車公司的收費標準如圖,其中x(km)表示行駛里程,y(元)表示車費,若乘客在打車后付費42元,則該乘客乘坐出租車行駛了25km.
某出租車公司的收費標準如圖,其中x(km)表示行駛里程,y(元)表示車費,若乘客在打車后付費42元,則該乘客乘坐出租車行駛了25km. 分析 根據待定系數法得到一次函數的解析式y=$\frac{3}{2}$x+$\frac{9}{2}$,當y=42時,得到方程$\frac{3}{2}$x+$\frac{9}{2}$=42,于是得到結論.
解答 解:∵42元>9元,
∴車費y是里程x的一次函數,
設y=kx+b,
∵直線經過(3,9),(5,12)兩點,
∴$\left\{\begin{array}{l}{9=3k+b}\\{12=5k+b}\end{array}\right.$,
∴$\left\{\begin{array}{l}{k=\frac{3}{2}}\\{b=\frac{9}{2}}\end{array}\right.$
∴y=$\frac{3}{2}$x+$\frac{9}{2}$,
當y=42時,即$\frac{3}{2}$x+$\frac{9}{2}$=42,
解得:x=25,
∴該乘客乘坐出租車行駛了25km,
故答案為:25.
點評 本題考查了函數的圖象,待定系數法求一次函數的解析式,求得一次函數的解析式是解題的關鍵.


 同步練習強化拓展系列答案
同步練習強化拓展系列答案科目:初中數學 來源: 題型:選擇題
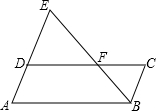 如圖,點F是?ABCD的邊CD上一點,直線BF交AD的延長線于點E,則下列結論錯誤的是( )
如圖,點F是?ABCD的邊CD上一點,直線BF交AD的延長線于點E,則下列結論錯誤的是( )| A. | $\frac{ED}{EA}$=$\frac{DF}{AB}$ | B. | $\frac{DE}{CB}$=$\frac{EF}{FB}$ | C. | $\frac{BF}{BE}$=$\frac{BC}{AE}$ | D. | $\frac{BC}{DE}$=$\frac{BF}{BE}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 0 | B. | 1 | C. | -1 | D. | 2014 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
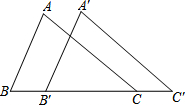 如圖,在△ABC中,AB=8,BC=12,∠B=60°,將△ABC沿著射線BC的方向平移4個單位后,得到△A'B'C',連接AC,則△A'B'C的面積是( )
如圖,在△ABC中,AB=8,BC=12,∠B=60°,將△ABC沿著射線BC的方向平移4個單位后,得到△A'B'C',連接AC,則△A'B'C的面積是( )| A. | 16 | B. | $4\sqrt{3}$ | C. | $16\sqrt{3}$ | D. | $32\sqrt{3}$ |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com