Question

3．等腰△ABC、△EFC中，AB=AC，FE=FC，D為BE的中點，∠BAC+∠EFC=180°，求證：AD⊥FD．

Answer 1

分析 延長FD到M，使得DM=DF，連接BM、AM、AF，延長BA交FE于H，AC與FH交于點O．想辦法證明△ABM≌△ACF，推出AM=AF即可解決問題．

解答 證明：延長FD到M，使得DM=DF，連接BM、AM、AF，延長BA交FE于H，AC與FH交于點O．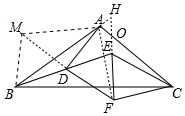

在△BDM和△EDF中，
$\left\{\begin{array}{l}{BD=DE}\\{∠BDM=∠EDF}\\{DM=DF}\end{array}\right.$，
∴△BDM≌△EDF，
∴EF=BM=CF，∠DBM=∠DEF，
∴BM∥EF，
∴∠ABM=∠H，
∵∠BAC+∠EFC=180°，∠BAC+∠HAO=180°，
∴∠HAO=∠OFC，∵∠AOH=∠COF，
∴∠H=∠ACF，
∴∠ABM=∠ACF，
在△ABM和△ACF中，
$\left\{\begin{array}{l}{AB=AC}\\{∠ABM=∠ACF}\\{BM=CF}\end{array}\right.$，
∴△ABM≌△ACF，
∴AM=AF，∵DF=DM，
∴AD⊥DF．

點評 本題考查全等三角形的判定和性質、等腰三角形的判定和性質、同角的補角相等等知識，解題的關鍵是學會添加常用輔助線，構造全等三角形解決問題，屬于中考常考題型．