
| A. | 130° | B. | 80° | C. | 140°或40° | D. | 60°或120° |
分析 作出圖形,設兩角平分線相交于點O,根據三角形的內角和定理求出∠ABC+∠ACB的度數,再根據角平分線的定義求出∠OBC+∠OCB的度數,然后在△BOC中利用三角形的內角和定理求解即可得到∠BOC的度數,再分夾角為鈍角與銳角兩種情況解答.
解答 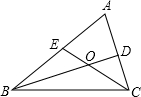 解:如圖,∵∠A=100°,
解:如圖,∵∠A=100°,
∴∠ABC+∠ACB=180°-∠A=180°-100°=80°,
∵BD、CE分別為∠ABC、∠ACB的平分線,
∴∠OBC=$\frac{1}{2}$∠ABC,∠OCB=$\frac{1}{2}$∠ACB,
∴∠OBC+∠OCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×80°=40°,
在△BOC中,∠BOC=180°-(∠OBC+∠OCB)=180°-40°=140°,
又∵180°-140°=40°,
∴∠B、∠C的平分線的夾角是140°或40°.
故選C.
點評 本題考查了三角形的角平分線的定義,三角形的內角和定理,整體思想的利用比較關鍵,要注意夾角有鈍角與銳角兩種情況.


科目:初中數學 來源: 題型:解答題
| 星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
| 增減 | +5 | -2 | -4 | +13 | -10 | +16 | -9 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 向西走110米 | B. | 向西走50米 | C. | 向西走30米 | D. | 向東走30米 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | $\frac{1}{5}$千米 | B. | $\frac{1}{14}$千米 | C. | $\frac{5}{14}$千米 | D. | $\frac{14}{5}$千米 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
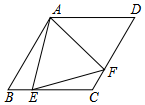 如圖,菱形ABCD中,∠B=60°,點E在邊BC上,點F在邊CD上.若EB=2,DF=3,∠EAF=60°,則△AEF的面積等于$\frac{19\sqrt{3}}{4}$.
如圖,菱形ABCD中,∠B=60°,點E在邊BC上,點F在邊CD上.若EB=2,DF=3,∠EAF=60°,則△AEF的面積等于$\frac{19\sqrt{3}}{4}$.查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com