
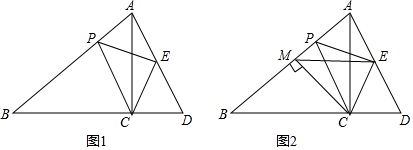
分析 (1)由∠PCD=∠B+∠BPC=∠PCE+∠ECD可知,只要證明∠B=∠PCE=45°即可.
(2)如圖2中,作EK⊥AB于K,EH⊥CM于H.由△EKP≌△EHC,推出EK=EH,因為EK⊥AB于K,EH⊥CM于H.所以∠EMK=∠EMC=45°,推出∠AME=∠B,推出ME∥BC,由CA=CB,CM⊥AB,推出AM=BM,CM=AM=BM,推出AE=ED,在Rt△ACD中,EC=AE=ED,此MA=MC,由此推出ME垂直平分線段AC.
(3)結論:PB2+AP2=2PC2.如圖3中,將△ACP繞點C逆時針旋轉90°得到△BCN.由∠ABC=∠CBN=45°,推出∠PBN=90°,推出PB2+BN2=PN2,由PC=CN,∠ACP=∠BCN,推出∠PCN=∠ACB=90°,推出PN=$\sqrt{2}$PC,AN=BN,即可推出PB2+AP2=2PC2.
解答 (1)解:結論:∠BPC=∠ECD.
理由:如圖1中,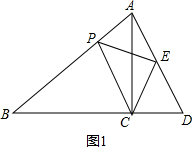
∵CA=CB,∠ACB=90°,
∴∠B=∠CAB=45°,
∵EP=EC,∠PEC=90°,
∴∠EPC=∠ECP=45°,
∵∠PCD=∠B+∠BPC=∠PCE+∠ECD,
∵∠B=∠PCE=45°,
∴∠BPC=∠ECD.
(2)證明:如圖2中,作EK⊥AB于K,EH⊥CM于H.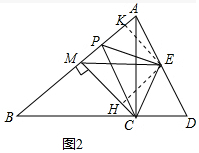
∵∠PMC+∠PEC=180°,
∴∠MPE+∠ECH=180°,
∵∠EPK+∠MPE=180°,
∴∠EPK=∠ECH,
∵∠EKP=∠EHC=90°,EP=EC,
∴△EKP≌△EHC,
∴EK=EH,∵EK⊥AB于K,EH⊥CM于H.
∴∠EMK=∠EMC=45°,
∴∠AME=∠B,
∴ME∥BC,
∵CA=CB,CM⊥AB,
∴AM=BM,CM=AM=BM,
∴AE=ED,
在Rt△ACD中,EC=AE=ED,
∵MA=MC,
∴ME垂直平分線段AC.
(3)解:結論:PB2+AP2=2PC2.
理由:如圖3中,將△ACP繞點C逆時針旋轉90°得到△BCN.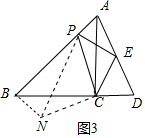
則∵∠ABC=∠CBN=45°,
∴∠PBN=90°,
∴PB2+BN2=PN2,
∵PC=CN,∠ACP=∠BCN,
∴∠PCN=∠ACB=90°,
∴PN=$\sqrt{2}$PC,AN=BN,
∴PB2+AP2=2PC2.
點評 本題考查全等三角形的判定和性質、等腰直角三角形的性質、角平分線的判定定理、勾股定理等知識,解題的關鍵是學會添加常用輔助線,構造全等三角形解決問題,學會用旋轉法添加輔助線構造全等三角形,屬于中考壓軸題.


科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
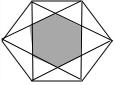 如圖,邊長為a的正六邊形中,連接一些頂點,中間圍成一個新的小正六邊形(陰影部分),則$\frac{{l}_{外部正六邊形}}{{l}_{陰影}}$(l為周長)等于( )
如圖,邊長為a的正六邊形中,連接一些頂點,中間圍成一個新的小正六邊形(陰影部分),則$\frac{{l}_{外部正六邊形}}{{l}_{陰影}}$(l為周長)等于( )| A. | 3 | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 若|a|=-a,則a<0 | B. | 若a<0,ab<0,則b>0 | ||
| C. | 若ab>0,則a>0,b>0 | D. | 若a=b,m是有理數,則$\frac{a}{m}$=$\frac{b}{m}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com