Question

1．已知如圖1，在以O為原點的平面直角坐標系中，拋物線y=$\frac{1}{4}$x²+bx+c與x軸交于A，B兩點，與y軸交于點C（0，-1），連接AC，AO=2CO，直線l過點G（0，t）且平行于x軸，t＜-1．
（1）求拋物線對應的二次函數的解析式；
（2）①若D（-4，m）為拋物線y=$\frac{1}{4}$x²+bx+c上一定點，點D到直線l的距離記為d，當d=DO時，求t的值；
②若為拋物線y=$\frac{1}{4}$x²+bx+c上一動點，點D到①中的直線l的距離與OD的長是否恒相等，說明理由；
（3）如圖2，若E，F為上述拋物線上的兩個動點，且EF=8，線段EF的中點為M，求點M縱坐標的最小值．

Answer 1

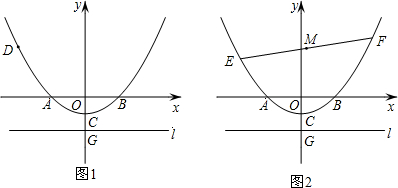
分析 （1）根據點C坐標，可得c=-1，然后根據AO=2CO，可得出點A坐標，將點A坐標代入求出b值，即可得出函數解析式；
（2）①設出點D坐標，分別求出OD和點D到直線l的距離，然后列出等式求出t的值；
②利用勾股定理得出OD²的值，進而得出答案；
（3）作EN⊥直線l于點N，FH⊥直線l于點H，設出點E、F坐標，表示出點M的縱坐標，根據（2）中得出的結果，代入結果求出M縱坐標的最小值．

解答 解（1）∵AO=2CO，C（0-1），
∴OA=2，A（-2，0），
將（0，-1），（-2，0）代入y=$\frac{1}{4}$x²+bx+c得：
$\left\{\begin{array}{l}{c=-1}\\{1-2b+c=0}\end{array}\right.$，
解得：$\left\{\begin{array}{l}{b=0}\\{c=-1}\end{array}\right.$
故拋物線解析式為：y=$\frac{1}{4}$x²-1；

（2）①由拋物線得：y=$\frac{1}{4}$×4²-1=3，
故D（-4，3）
則OD=5，
又∵d=DO
∴t=3-5=-2，

②設D（a，$\frac{1}{4}$a²-1）
則OD²=a²+（$\frac{1}{4}$a²-1）²
=a²+$\frac{1}{16}$a⁴-$\frac{1}{2}$a²+1
=（$\frac{1}{4}$a²+1）²，
點D到直線l的距離：$\frac{1}{4}$a²-1+2=$\frac{1}{4}$a²+1，
故d=DO；

（3）作EN⊥直線l于點N，FH⊥直線l于點H，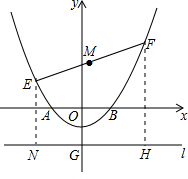
設E（x₁，y₁），F（x₂，y₂），
則EN=y₁+2，FH=y₂+2，
∵M為EF中點，
∴M縱坐標為：$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{（EN-2）+（FH-2）}{2}$=$\frac{EN+FH}{2}$-2，
由（2）得：EN=OE，FH=OF，
∴$\frac{{y}_{1}+{y}_{2}}{2}$=$\frac{EN+FH}{2}$-2=$\frac{OE+OF}{2}$-2，
要使M縱坐標最小，即$\frac{OE+OF}{2}$-2最小，
當EF過點O時，OE+OF最小，最小值為8，
∴M縱坐標最小值為$\frac{OE+OF}{2}$-2=$\frac{8}{2}$-2=2．

點評 本題考查了二次函數的綜合知識，涉及到拋物線解析式的求法，點到直線的距離、兩點間的距離等知識，涉及到的知識點比較多，利用數形結合表示出M點縱坐標是解題關鍵．