
 你能證明你所得出的結論嗎?
你能證明你所得出的結論嗎?分析 連接AC.根據ASA證明△ABC≌△CDA即可解決問題.
解答 解:如圖連接AC.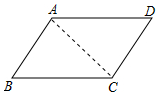
∵四邊形ABCD是平行四邊形,
∵AB∥CD,AD∥BC,
∴∠BADBAC=∠ACD,∠BCA=∠CAD,
在△ABC和△CDA中,
$\left\{\begin{array}{l}{∠BAC=∠ACD}\\{AC=CA}\\{∠BCA=∠CAD}\end{array}\right.$,
∴△ABC≌△CDA,
∴AB=CD,BC=AD,∠B=∠D,
∵∠BAC=∠ACD,∠BCA=∠CAD,
∠BAD=∠BCD.
故答案分別為≌,AB=CD,BC=AD;∠B=∠D,∠BAD=∠BCD;平行四邊形的對邊相等,平行四邊形的對角相等.
點評 本題考查全等三角形的判定和性質、平行四邊形的判定和性質等知識,解題的關鍵是學會用轉化的思想思考問題,把四邊形問題轉化為三角形問題,屬于中考常考題型.


科目:初中數學 來源: 題型:選擇題
 實數a,b,c在數軸上對應的點如圖所示,則下列式子中正確的是( )
實數a,b,c在數軸上對應的點如圖所示,則下列式子中正確的是( )| A. | a-c>b-c | B. | $\frac{a}{b}$<$\frac{c}{b}$ | C. | ac>bc | D. | a+c<b+c |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
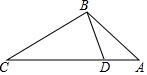 如圖,點D在△ABC的邊AC上,要判定△ADB與△ABC相似,添加一個條件,不正確的是( )
如圖,點D在△ABC的邊AC上,要判定△ADB與△ABC相似,添加一個條件,不正確的是( )| A. | ∠ABD=∠C | B. | ∠ADB=∠ABC | C. | $\frac{AB}{BD}=\frac{CB}{CA}$ | D. | $\frac{AB}{AD}=\frac{AC}{AB}$ |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
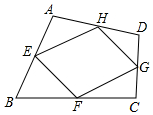 如圖,四邊形ABCD中,E,F,G,H分別是AB,BC,CD,AD邊的中點,AC=6,BD=8,那么四邊形EFGH的周長是( )
如圖,四邊形ABCD中,E,F,G,H分別是AB,BC,CD,AD邊的中點,AC=6,BD=8,那么四邊形EFGH的周長是( )| A. | 20 | B. | 28 | ||
| C. | 14 | D. | 以上答案均有可能 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 向左平移1個單位,再向上平移1個單位 | |
| B. | 向右平移1個單位,再向下平移1個單位 | |
| C. | 向左平移1個單位,再向下平移1個單位 | |
| D. | 向右平移1個單位,再向上平移1個單位 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com