
分析 先找規律,得到通項公式,然后再運用公式解決問題
解答 解:因為①可變形為若ab=12時,a+b≥1×2,即a+b的最小值為2.
②可變形為若ab=22時,a+b≥2×2,即a+b的最小值為4.
③可變形為若ab=32時,a+b≥3×2,即a+b的最小值為6.
④可變形為若ab=42時,a+b≥4×2,即a+b的最小值為8.
根據以上所提供的規律猜想:若a>0,b>0,ab=n2時,a+b≥n×2,即a+b的最小值為2n,
所以若a>0,b>0,且ab=102,a+b≥10×2,求a+b的最小值為20.
點評 本題考查了完全平方公式的變形a+b≥2$\sqrt{ab}$,根據已知找出規律是解決問題的關鍵.


科目:初中數學 來源: 題型:解答題
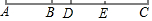 如圖,已知線段AB=3cm,延長線段AB到C,使BC=2AB.
如圖,已知線段AB=3cm,延長線段AB到C,使BC=2AB.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
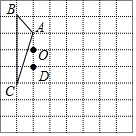 如圖,方格紙中的每個小方格都是邊長為1個單位長度的正方形,每個小正方形的頂點叫格點,△ABC的頂點均在格點上,請按要求完成下列步驟:
如圖,方格紙中的每個小方格都是邊長為1個單位長度的正方形,每個小正方形的頂點叫格點,△ABC的頂點均在格點上,請按要求完成下列步驟:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,已知A,B兩點在數軸上,點A表示的數為-10,OB=3OA,點M以每秒3個單位長度的速度從點A向右運動.點N以每秒2個單位長度的速度從點O向右運動(點M、點N同時出發)
如圖,已知A,B兩點在數軸上,點A表示的數為-10,OB=3OA,點M以每秒3個單位長度的速度從點A向右運動.點N以每秒2個單位長度的速度從點O向右運動(點M、點N同時出發)查看答案和解析>>
科目:初中數學 來源: 題型:解答題
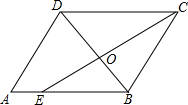 如圖,在平行四邊形ABCD中,CE是∠DCB的角平分線,且交AB于點E,DB與CE相交于點O,
如圖,在平行四邊形ABCD中,CE是∠DCB的角平分線,且交AB于點E,DB與CE相交于點O,查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com