
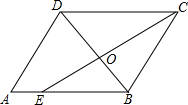
 如圖,在平行四邊形ABCD中,CE是∠DCB的角平分線,且交AB于點E,DB與CE相交于點O,
如圖,在平行四邊形ABCD中,CE是∠DCB的角平分線,且交AB于點E,DB與CE相交于點O,分析 (1)欲證明△EBC是等腰三角形,只需推知BC=BE即可,可以由∠2=∠3得到:BC=BE;
(2)通過相似三角形(△COD∽△EOB)的對應邊成比例得到$\frac{CD}{EB}$=$\frac{OD}{OB}$=$\frac{7}{5}$,然后利用分式的性質(zhì)可以求得$\frac{OB}{DB}$=$\frac{5}{12}$.
解答 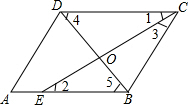 證明:(1)∵四邊形ABCD是平行四邊形,
證明:(1)∵四邊形ABCD是平行四邊形,
∴CD∥AB,
∴∠1=∠2.
∵CE平分∠BCD,
∴∠1=∠3,
∴∠2=∠3,
∴BC=BE,
∴△EBC是等腰三角形;
解:(2)∵∠1=∠2,∠4=∠5,
∴△COD∽△EOB,
∴$\frac{CD}{EB}$=$\frac{OD}{OB}$.
∵平行四邊形ABCD,
∴CD=AB=7.
∵BE=BC=5,
∴$\frac{CD}{EB}$=$\frac{OD}{OB}$=$\frac{7}{5}$,
∴$\frac{OB}{DB}$=$\frac{5}{12}$.
點評 本題考查了平行四邊形的性質(zhì),相似三角形的判定與性質(zhì)以及等腰三角形的判定.在判定兩個三角形相似時,應注意利用圖形中已有的公共角、公共邊等隱含條件,以充分發(fā)揮基本圖形的作用,尋找相似三角形的一般方法是通過作平行線構(gòu)造相似三角形;在運用三角形相似的性質(zhì)時主要利用相似比計算相應線段的長.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
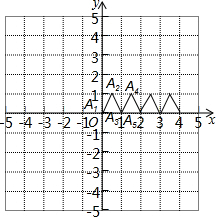 一只電子青蛙在如圖的平面直角坐標系做如下運動:從坐標原點開始起跳記為A1,然后沿著邊長為1的等邊三角形跳躍即A1→A2→A3→A4→A5…已知A3的坐標為(1,0),則A2014的坐標是(1006,$\frac{\sqrt{3}}{2}$).
一只電子青蛙在如圖的平面直角坐標系做如下運動:從坐標原點開始起跳記為A1,然后沿著邊長為1的等邊三角形跳躍即A1→A2→A3→A4→A5…已知A3的坐標為(1,0),則A2014的坐標是(1006,$\frac{\sqrt{3}}{2}$).查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com