
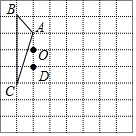
 如圖,方格紙中的每個小方格都是邊長為1個單位長度的正方形,每個小正方形的頂點叫格點,△ABC的頂點均在格點上,請按要求完成下列步驟:
如圖,方格紙中的每個小方格都是邊長為1個單位長度的正方形,每個小正方形的頂點叫格點,△ABC的頂點均在格點上,請按要求完成下列步驟:分析 (1)利用網格特點和旋轉的性質畫出點A、B、C的對應點A′、B′、C′即可;
(2)利用弧長公式求解;
(3)把BC分為兩段BC′、CC′,然后利用扇形的面積之差分別計算BC′、CC′所掃過的面積;
(4)延長AO到A″使OA″=2OA,則點A″為點A的對應點,同樣方法作出B、C的對應點B″、C″,從而得到△A″B″C″.
解答 解:(1)如圖,△A′B′C′為所作;
(2)DC=$\sqrt{2}$,
所以點C所經過的路徑長=$\frac{90•π•\sqrt{2}}{180}$=$\frac{\sqrt{2}}{2}$π;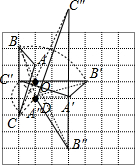
(3)DB=$\sqrt{{1}^{2}+{3}^{2}}$=$\sqrt{10}$,
所以線段BC旋轉過程中掃過的面積=2[$\frac{90•π•(\sqrt{2})^{2}}{360}$-$\frac{90•π•{1}^{2}}{360}$]+[$\frac{90•π•(\sqrt{10})^{2}}{360}$-$\frac{90•π•(\sqrt{2})^{2}}{360}$]=$\frac{5}{2}$π;
(4)如圖,△A″B″C″為所作.
點評 本題考查了作圖-位似變換:畫位似圖形的一般步驟為:先確定位似中心;再分別連接并延長位似中心和能代表原圖的關鍵點;接著根據位似比,確定能代表所作的位似圖形的關鍵點;然后順次連接上述各點,得到放大或縮小的圖形.也考查了軸對稱變換和旋轉變換.


 世紀百通主體課堂小學課時同步達標系列答案
世紀百通主體課堂小學課時同步達標系列答案 世紀百通優練測系列答案
世紀百通優練測系列答案 百分學生作業本題練王系列答案
百分學生作業本題練王系列答案科目:初中數學 來源: 題型:解答題
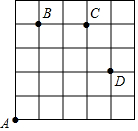 如圖,一只甲蟲在5×5的方格(每小格邊長為1)上沿著網格線運動.它從A處出發去看望B、C、D處的其它甲蟲,規定:向上向右走均為正,向下向左走均為負.如果從A到B記為:A→B(+1,+4),從B到A記為:B→A(-1,-4),其中第一個數表示左右方向,第二個數表示上下方向.
如圖,一只甲蟲在5×5的方格(每小格邊長為1)上沿著網格線運動.它從A處出發去看望B、C、D處的其它甲蟲,規定:向上向右走均為正,向下向左走均為負.如果從A到B記為:A→B(+1,+4),從B到A記為:B→A(-1,-4),其中第一個數表示左右方向,第二個數表示上下方向.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
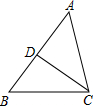 如圖,D是△ABC的邊AB上的一點,BD=$\frac{4}{3}$,AB=3,BC=2
如圖,D是△ABC的邊AB上的一點,BD=$\frac{4}{3}$,AB=3,BC=2查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
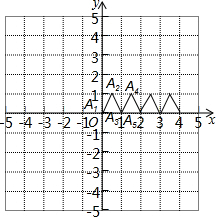 一只電子青蛙在如圖的平面直角坐標系做如下運動:從坐標原點開始起跳記為A1,然后沿著邊長為1的等邊三角形跳躍即A1→A2→A3→A4→A5…已知A3的坐標為(1,0),則A2014的坐標是(1006,$\frac{\sqrt{3}}{2}$).
一只電子青蛙在如圖的平面直角坐標系做如下運動:從坐標原點開始起跳記為A1,然后沿著邊長為1的等邊三角形跳躍即A1→A2→A3→A4→A5…已知A3的坐標為(1,0),則A2014的坐標是(1006,$\frac{\sqrt{3}}{2}$).查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com