
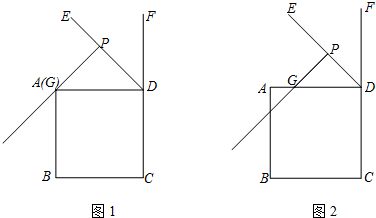
分析 (1)①依題意補全圖形即可;
②由正方形的性質和角平分線得出∠EDF=∠ADE=45°,證出∠HAD=∠PDC,∠ADQ=∠DCQ,由ASA證明△HAD≌△PDC,得出對應邊相等即可;
(2)思路如下:a、與②同理可證∠HGD=∠PDC,∠ADQ=∠DCP,可證△HGD∽△PDC;b、由②可知△GPD為等腰直角三角形,可設DP=PG=x,則GD=$\sqrt{2}$x,AG=1-$\sqrt{2}$x,易證△AGH為等腰直角三角形,則GH=$\sqrt{2}$-2x;c、由△HGD∽△PDC得出比例式,解方程即可求得DP的長.
解答 解:(1)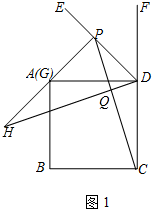 ①依題意補全圖1,如圖1所示:
①依題意補全圖1,如圖1所示:
②DH=PC,理由如下:
∵DE為正方形的外角∠ADF的角平分線,
∴∠EDF=∠ADE=45°,
∵PG⊥DE于點P,
∴∠DAP=45°,
∴∠HAD=135°,∠PDC=135°,
∴∠HAD=∠PDC,
∵四邊形ABCD為正方形,
∴AD=CD,
∵DQ⊥PC,
∴∠CDQ+∠DCQ=90°,
∵∠ADQ+∠CDQ=90°,
∴∠ADQ=∠DCQ,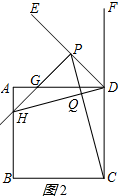
在△HAD和△PDC中,
$\left\{\begin{array}{l}{∠HAD=∠PDC}\\{AD=CD}\\{∠ADQ=∠DCQ}\end{array}\right.$,
∴△HAD≌△PDC(ASA),
∴DH=CP;
(2)求DP長的思路如下:如圖2所示:
a、與②同理得:∠HGD=∠PDC,∠ADQ=∠DCP,
∴△HGD∽△PDC;
b、由②可知△GPD為等腰直角三角形,
∴∠AGH=∠PGD=45°,
∴△AGH為等腰直角三角形,
設DP=PG=x,則GD=$\sqrt{2}$x,AG=1-$\sqrt{2}$x,GH=$\sqrt{2}$-2x;
c、由△HGD∽△PDC得:$\frac{GH}{DP}=\frac{GD}{DC}$,
即$\frac{\sqrt{2}-2x}{x}$=$\frac{\sqrt{2}x}{1}$,
解得:x=$\frac{-\sqrt{2}±\sqrt{6}}{2}$(負值舍去),
∴DP=$\frac{\sqrt{6}-\sqrt{2}}{2}$.
點評 本題是四邊形綜合題目,考查了正方形的性質、全等三角形的判定與性質、勾股定理、等腰直角三角形的判定與性質、相似三角形的判定與性質等知識;本題綜合性強,難度較大,熟練掌握正方形的性質,證明三角形全等和三角形相似是解決問題的關鍵.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (1)如圖,把∠AOB繞著O點按逆時針方向旋轉一個角度,得∠A′OB′,指出圖中所有相等的角.
(1)如圖,把∠AOB繞著O點按逆時針方向旋轉一個角度,得∠A′OB′,指出圖中所有相等的角.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
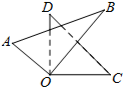 如圖是由一副三角尺拼成的圖案,它們有公共頂點O,且有一部分重疊,已知∠BOD=40°,則∠AOC的度數是( )
如圖是由一副三角尺拼成的圖案,它們有公共頂點O,且有一部分重疊,已知∠BOD=40°,則∠AOC的度數是( )| A. | 40° | B. | 120° | C. | 140° | D. | 150° |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com