
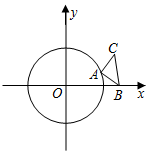
 如圖,⊙O的半徑為1,等腰直角三角形ABC的頂點B固定且坐標為($\sqrt{2}$,0),頂點A在⊙O上運動,始終保持∠CAB=90°,AC=AB
如圖,⊙O的半徑為1,等腰直角三角形ABC的頂點B固定且坐標為($\sqrt{2}$,0),頂點A在⊙O上運動,始終保持∠CAB=90°,AC=AB分析 (1)中有兩種情況,即A點坐標為(1,0)或(-1,0),根據AB=AC,求出C點坐標;
(2)根據題意過點O作OM⊥BC于點M,求出OM的長,與半徑比較得出位置關系;
(3)過點A作AE⊥OB于點E,在Rt△OAE中求AE的長,然后再在Rt△BAE中求出AB的長,進而求出面積的表達式,根據自變量的取值范圍確定最大最小值;
(4)相切時有兩種情況,在第一象限或者第四象限,連接OA,并過點A作AE⊥OB于點E,在Rt△OAE中求出OE,然后就能求出A點坐標,AB所在直線對應的函數關系式很容易就能求出.
解答 解:
(1)當點A的坐標為(1,0)時,AB=AC=$\sqrt{2}$-1,點C的坐標為(1,$\sqrt{2}$-1)或(1,1-$\sqrt{2}$);
當點A的坐標為(-1,0)時,AB=AC=$\sqrt{2}$+1,點C的坐標為(-1,$\sqrt{2}$+1)或(-1,-$\sqrt{2}$-1);
(2)直線BC與⊙O相切.
如圖1,過點O作OM⊥BC于點M,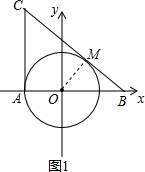
∴∠OBM=∠BOM=45°,
∴OM=OB•sin45°=1
∴直線BC與⊙O相切;
(3)過點A作AE⊥OB于點E,如圖2,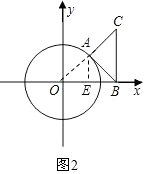
在Rt△OAE中,AE2=OA2-OE2=1-x2,
在Rt△BAE中,AB2=AE2+BE2=(1-x2)+($\sqrt{2}$-x)2=3-2$\sqrt{2}$x
∴S=$\frac{1}{2}$AB•AC=$\frac{1}{2}$AB2=$\frac{1}{2}$(3-2$\sqrt{2}$x)=$\frac{3}{2}$-$\sqrt{2}$x,
其中-1≤x≤1,
當x=-1時,S的最大值為$\frac{3}{2}$+$\sqrt{2}$,
當x=1時,S的最小值為$\frac{3}{2}$-$\sqrt{2}$;
(4)①當點A位于第一象限時(如右圖3):
連接OA,并過點A作AE⊥OB于點E,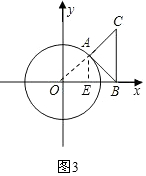
∵直線AB與⊙O相切,
∴∠OAB=90°,
又∵∠CAB=90°,
∴∠CAB+∠OAB=180°,
∴點O、A、C在同一條直線
∴∠AOB=∠C=45°,即∠CBO=90°,
在Rt△OAE中,OE=AE=$\frac{\sqrt{2}}{2}$,
點A的坐標為($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{2}}{2}$)
過A、B兩點的直線為y=-x+$\sqrt{2}$;
②當點A位于第四象限時(如圖4),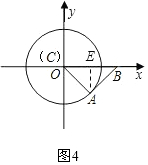
點A的坐標為($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$)
∵B的坐標為($\sqrt{2}$,0)
∴過A、B兩點的直線為y=x-$\sqrt{2}$.
點評 本題為圓的綜合應用,涉及切線的性質與判定、直線與圓的位置關系、等腰直角三角形的性質以及待定系數法求一次函數解析式等知識.此題難度較大,注意掌握輔助線的作法,注意掌握方程思想、分類討論思想與數形結合思想的應用.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 1 | B. | -1 | C. | 1或-1 | D. | 不確定 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com