
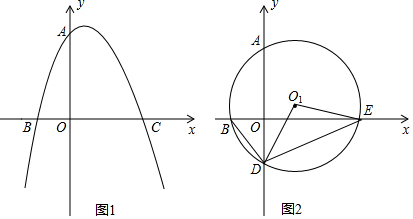
分析 (1)利用待定系數法即可即可解決問題.
(2)如圖1中,連接AB、AC、作MD⊥x軸于D,首先證明∠OAC=∠DMC=45°,再證明△AOB∽△MDN,推出$\frac{OA}{DM}$=$\frac{OB}{DN}$,求得DN=2,即可解決問題.
(3)如圖3中,連接AB、作O1N⊥DE于N.由△AOB∽△EOD,推出$\frac{AO}{OE}$=$\frac{OB}{OD}$,推出OE=2OD,設OD=k,則OE=2k,DE=$\sqrt{5}$k,由△BOD∽△O1ND,推出$\frac{{S}_{△D{O}_{1}N}}{{S}_{△BOD}}$=($\frac{DN}{OD}$)2=($\frac{\frac{\sqrt{5}}{2}k}{k}$)2=$\frac{5}{4}$,由此即可解決問題.
解答 解:(1)把M(-2,-4),B(-1,0)點坐標代入y=-x2+bx+c得到$\left\{\begin{array}{l}{-4-2b+c=-4}\\{-1-b+c=0}\end{array}\right.$,
解得$\left\{\begin{array}{l}{b=1}\\{c=2}\end{array}\right.$,
∴拋物線的解析式為y=-x2+x+2.
(2)如圖1中,連接AB、AC、作MD⊥x軸于D.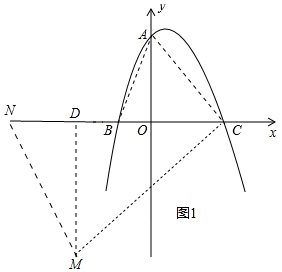
對于拋物線y=-x2+x+2,令y=0,-x2+x+2=0,解得x=-1或2,
∴C(2,0),
∴OA=OC=2,DM=DC=4,
∴∠OAC=∠DMC=45°,
∵∠NMC=∠BAC,
∴∠NMD=∠BAO,∵∠AOB=∠MDN=90°,
∴△AOB∽△MDN,
∴$\frac{OA}{DM}$=$\frac{OB}{DN}$,
∴$\frac{2}{4}$=$\frac{1}{DN}$,
∴DN=2,
∴ON=4,
∴點N的坐標為(-4,0).
(3)如圖3中,連接AB、作O1N⊥DE于N.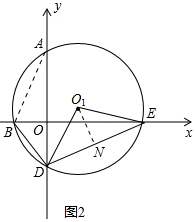
∵∠AOB=∠DOE,∠BAO=∠OED,
∴△AOB∽△EOD,
∴$\frac{AO}{OE}$=$\frac{OB}{OD}$,
∴$\frac{2}{OE}$=$\frac{1}{OD}$,
∴OE=2OD,設OD=k,則OE=2k,DE=$\sqrt{5}$k,
∵O1N⊥DE,
∴DN=EN,∠DO1N=∠EO1N,
∵∠DO1E=2∠DBE,
∴∠OBD=∠DO1N,
∵∠BOD=∠O1ND=90°,
∴△BOD∽△O1ND,
∴$\frac{{S}_{△D{O}_{1}N}}{{S}_{△BOD}}$=($\frac{DN}{OD}$)2=($\frac{\frac{\sqrt{5}}{2}k}{k}$)2=$\frac{5}{4}$,
∵${S}_{△{O}_{1}DE}$=2${S}_{△D{O}_{1}N}$,
∴$\frac{{S}_{△D{O}_{1}E}}{{S}_{△BOD}}$=$\frac{10}{4}$=$\frac{5}{2}$.
點評 本題考查二次函數綜合題、等腰直角三角形的性質、相似三角形的判定和性質、勾股定理垂徑定理等知識,解題的關鍵是正確尋找相似三角形解決問題,屬于中考壓軸題.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學生10分鐘應用題系列答案
小學生10分鐘應用題系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
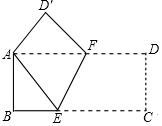 按如圖方式折疊長方形紙片ABCD,使頂點A、C重合(圖中點D落在點D′處,E,F分別是折痕與BC,AD的交點),已知AB=3,BC=9,求BE及折痕EF的長.
按如圖方式折疊長方形紙片ABCD,使頂點A、C重合(圖中點D落在點D′處,E,F分別是折痕與BC,AD的交點),已知AB=3,BC=9,求BE及折痕EF的長.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com