
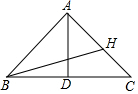
 如圖,在△ABC中,AB=10,BC=12,BC邊上的中線AD=8.
如圖,在△ABC中,AB=10,BC=12,BC邊上的中線AD=8.分析 (1)由三角形的中線的定義可知BD=DC=6,然后依據勾股定理的逆定理可證明△ABD為直角三角形,故此AD⊥BC,則AD為BC的垂直平分線,依據線段垂直平分線的性質可知AB=AC;
(2)由題意可得到CH+AC=AC=10,故此當BH最小時,AH+BH+CH有最小值,依據垂線段的性質可知當BH⊥AC時,BH有最小值,在△ABC中,依據面積法可求得BH的最小值.
解答 解:(1)∵AD是BC邊上的中線,
∴BD=DC=6.
在△ABD中,BD2+AD2=62+82=102=AB2,
∴△ABD為直角三角形.
∴∠ADB=90°.
∴AD⊥BC.
∵AD⊥BC,BD=DC,
∴AB=AC.
∴△ABC為等腰三角形.
(2)∵AH+BH+CH=AC+BH=10+BH,
∴當BH最小時,AH+BH+CH有最小值.
由垂線段的性質可知當BH⊥AC時,BH有最小值.
∴$\frac{1}{2}$BH•AC=$\frac{1}{2}$BC•AD,即$\frac{1}{2}$×10•BH=$\frac{1}{2}$×12×8,
解得:BH=9.6.
∴AH+BH+CH的最小值=10+9.6=19.6.
點評 本題主要考查的是最短路徑問題,解答本題主要應用了勾股定理的逆定理、線段垂直平分線的性質,垂線段的性質,明確當BH⊥AC時,AH+BH+CH有最小值是解題的關鍵.


 期末好成績系列答案
期末好成績系列答案 99加1領先期末特訓卷系列答案
99加1領先期末特訓卷系列答案 百強名校期末沖刺100分系列答案
百強名校期末沖刺100分系列答案 好成績1加1期末沖刺100分系列答案
好成績1加1期末沖刺100分系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
| m | 5 | -3 | -4 | -4 |
| n | 2 | 0 | 3 | -2 |
| A、B兩點間的距離 | 3 | 3 | 7 | 2 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 甲、乙兩人從A地出發,騎自行車在同一條路上行駛到B地,他們離出發地的距離s(千米)和行駛時間t(時)之間的關系的圖象如圖所示.根據圖中提供的信息,有下列說法:
甲、乙兩人從A地出發,騎自行車在同一條路上行駛到B地,他們離出發地的距離s(千米)和行駛時間t(時)之間的關系的圖象如圖所示.根據圖中提供的信息,有下列說法:| A. | 2個 | B. | 3個 | C. | 4個 | D. | 5個 |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com