
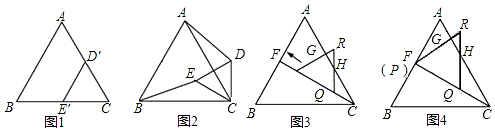
分析 (1)求兩條線段之間的關(guān)系,可先證明△BCE≌△ACD,進(jìn)而根據(jù)全等三角形的性質(zhì),得出兩條對應(yīng)邊之間的關(guān)系;
(2)等腰三角形的判定問題,可根據(jù)題中角之間的關(guān)系得出∠QHC=∠QCH,即可得到QH=QC,進(jìn)而判定△HQC為等腰三角形;
(3)根據(jù)等邊三角形的性質(zhì),求得BF=2=AF,再利用勾股定理以及含30°角的直角三角形的性質(zhì)進(jìn)行求解,或者根據(jù)(2)中的結(jié)論,即可得出QH的長度.
解答 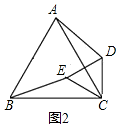 解:(1)BE=AD.
解:(1)BE=AD.
理由:由題意可得,BC=AC,CE=CD,
∵∠BCE+∠ACE=60°,∠ACE+∠ACD=60°
∴∠BCE=∠ACD,
在△BCE和△ACD中,
$\left\{\begin{array}{l}{BC=AC}\\{∠BCE=∠ACD}\\{CE=CD}\end{array}\right.$,
∴△BCE≌△ACD(SAS),
∴BE=AD;
(2)△HQC為等腰三角形.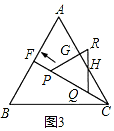
理由:∵∠FCB=30°,∠ACB=60°,
∴∠ACF=30°,
又∵∠RQP=60°,
∴∠QHC=60°-30°=30°,
∴∠QHC=∠QCH,
∴QH=QC,即△HQC為等腰三角形;
(3)解法1:∵∠BCF=30°,BC=4,∠B=60°,
∴Rt△BCF中,BF=2,CF=2$\sqrt{3}$,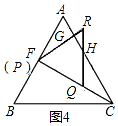
又∵FQ=3,
∴CQ=FC-FQ=2$\sqrt{3}$-3,
由(2)可得,HQ=CQ=2$\sqrt{3}$-3.
解法2:∵∠BCF=30°,BC=4,∠B=60°,
∴Rt△BCF中,BF=2=AF,
∴在Rt△AFG中,F(xiàn)G=$\sqrt{3}$,
∴GR=3-$\sqrt{3}$,
∵∠RHG=30°,
∴在Rt△GRH中,RH=2(3-$\sqrt{3}$),
∴HQ=3-2(3-$\sqrt{3}$)=2$\sqrt{3}$-3.
點(diǎn)評 本題屬于三角形綜合題,主要考查了全等三角形的判定與性質(zhì),等腰三角形的判定定理,等邊三角形的性質(zhì),勾股定理以及含30°角的直角三角形的性質(zhì)的綜合應(yīng)用.掌握兩邊及其夾角分別對應(yīng)相等的兩個三角形全等,是正確解答第(1)問的關(guān)鍵.在判定等腰三角形時(shí)注意:如果一個三角形有兩個角相等,那么這兩個角所對的邊也相等.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:填空題
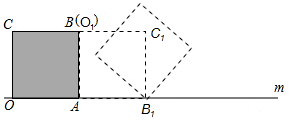 把邊長為1的正方形紙片PABC放在直線m上,OA邊在直線m上,然后將正方形紙片繞著頂點(diǎn)A按順時(shí)針方向旋轉(zhuǎn)90°,此時(shí),點(diǎn)O運(yùn)動到了點(diǎn)O1處(即點(diǎn)B處),點(diǎn)C運(yùn)動到了點(diǎn)C1處,點(diǎn)B運(yùn)動到了點(diǎn)B1處,又將正方形紙片AO1C1B1繞B1點(diǎn),按順時(shí)針方向旋轉(zhuǎn)90°…,按上述方法經(jīng)過2016次旋轉(zhuǎn)后,頂點(diǎn)O經(jīng)過的總路徑的長為(252$\sqrt{2}$+504)π.
把邊長為1的正方形紙片PABC放在直線m上,OA邊在直線m上,然后將正方形紙片繞著頂點(diǎn)A按順時(shí)針方向旋轉(zhuǎn)90°,此時(shí),點(diǎn)O運(yùn)動到了點(diǎn)O1處(即點(diǎn)B處),點(diǎn)C運(yùn)動到了點(diǎn)C1處,點(diǎn)B運(yùn)動到了點(diǎn)B1處,又將正方形紙片AO1C1B1繞B1點(diǎn),按順時(shí)針方向旋轉(zhuǎn)90°…,按上述方法經(jīng)過2016次旋轉(zhuǎn)后,頂點(diǎn)O經(jīng)過的總路徑的長為(252$\sqrt{2}$+504)π.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com