
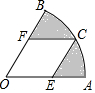
 如圖,在扇形OAB中,∠O=60°,OA=4$\sqrt{3}$,四邊形OECF是扇形OAB中最大的菱形,其中點E,C,F分別在OA,$\widehat{AB}$,OB上,則圖中陰影部分的面積為8π-8$\sqrt{3}$.
如圖,在扇形OAB中,∠O=60°,OA=4$\sqrt{3}$,四邊形OECF是扇形OAB中最大的菱形,其中點E,C,F分別在OA,$\widehat{AB}$,OB上,則圖中陰影部分的面積為8π-8$\sqrt{3}$. 分析 連接EF、OC交于點H,根據正切的概念求出FH,根據菱形的面積公式求出菱形FOEC的面積,根據扇形面積公式求出扇形OAB的面積,計算即可.
解答 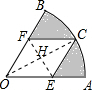 解:連接EF、OC交于點H,
解:連接EF、OC交于點H,
則OH=2$\sqrt{3}$,
∴FH=OH×tan30°=2,
∴菱形FOEC的面積=$\frac{1}{2}$×4$\sqrt{3}$×4=8$\sqrt{3}$,
扇形OAB的面積=$\frac{60π×(4\sqrt{3})^{2}}{360}$=8π,
則陰影部分的面積為8π-8$\sqrt{3}$,
故答案為:8π-8$\sqrt{3}$.
點評 本題考查的是扇形面積的計算、菱形的性質,掌握扇形的面積公式、菱形的性質、靈活運用銳角三角函數的定義是解題的關鍵.


 智能訓練練測考系列答案
智能訓練練測考系列答案科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com