
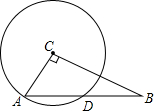
 ��֪����D����Rt��ABC�У���ACB=90�㣬AC=3��BC=4�����c(di��n)C��A�ģ�CA��돽�ĈA�cAB�����c(di��n)D��
��֪����D����Rt��ABC�У���ACB=90�㣬AC=3��BC=4�����c(di��n)C��A�ģ�CA��돽�ĈA�cAB�����c(di��n)D������ ��1���ȸ���(j��)���ɶ������AB���L(zh��ng)���^(gu��)C��CM��AB����AB���c(di��n)M���ɴ���������֪M��AD�����c(di��n)���������ε���e�����CM���L(zh��ng)����Rt��ACM�У�����(j��)���ɶ��������AM���L(zh��ng)���M(j��n)���ɵó��Y(ji��)Փ��
��2������(j��)���������ε����|(zh��)�������εă�(n��i)�Ǻ͵õ���ACD=34�㣬���ǵõ��Y(ji��)Փ��
��3������(j��)�}�⼴�ɵõ��Y(ji��)Փ��
��� �⣺����Rt��ABC�У���ACB=90�㣬AC=3��BC=4��
��AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=5��
�^(gu��)C��CM��AB����AB���c(di��n)M����D��ʾ��
��CM��AB��
��M��AD�����c(di��n)��
��S��ABC=$\frac{1}{2}$AC•BC=$\frac{1}{2}$AB•CM����AC=3��BC=4��AB=5��
��CM=$\frac{12}{5}$��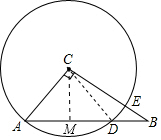
��Rt��ACM�У�����(j��)���ɶ����ã�AC2=AM2+CM2����9=AM2+��$\frac{12}{5}$��2��
��ã�AM=$\frac{9}{5}$��
��AD=2AM=$\frac{18}{5}$��
��2���ߡ�ACB=90�㣬��B=28�㣬
���A=62�㣬
�B��CD��
��AC=CD��
���CDA=��A=28�㣬
���ACD=34�㣬
�$\widehat{AD}$�ĶȔ�(sh��)��34�㣻
��3������CP���L(zh��ng)��ȡֵ������$\frac{18}{5}$��CP��4��
�ʴ𰸞飺$\frac{18}{5}$��CP��4��
�c(di��n)�u(p��ng) ���}������Ǵ������������������ε����|(zh��)�������εă�(n��i)�Ǻͣ�����(j��)�}�������o��������(g��u)���ֱ���������ǽ����}���P(gu��n)�I��


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
С�W(xu��)��10��犑�(y��ng)���}ϵ�д�
| �꼉(j��) | �����n�� | �꼉(j��) | �����n�� |
| ��һ | ��һ���M(f��i)�n�����]�� | ��һ | ��һ���M(f��i)�n�����]�� |
| �߶� | �߶����M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
| ���� | �������M(f��i)�n�����]�� | ���� | �������M(f��i)�n�����]�� |
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ��x���}
| A�� | x=2 | B�� | x=-2 | C�� | x=1 | D�� | x=-1 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
| �\(y��n)����� | ���� | �����(c��)����ʽ�������e�� |
| �ٽo������һ��(g��)��λ��(sh��) | 325 | 123 |
| ���؏�(f��)���еĔ�(sh��)���õ�һ��(g��)�µĔ�(sh��)�� | 325325 | 123123 |
| �ی��ڵĽY(ji��)������7 | 325325��7=a46475 | 123123��7=17589 |
| �܌��۵ĽY(ji��)������11 | a��11=b4225 | 17589��11=1599 |
| ���ܵĽY(ji��)������13 | b��13=325 | 1599��13=123 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ��x���}
 ��D���c(di��n)A��D��G��M�ڰ�AO�ϣ���߅��ABOC��DEOF��HMNO������Σ��O(sh��)BC=a��EF=b��NH=c���t���и�ʽ�����_���ǣ�������
��D���c(di��n)A��D��G��M�ڰ�AO�ϣ���߅��ABOC��DEOF��HMNO������Σ��O(sh��)BC=a��EF=b��NH=c���t���и�ʽ�����_���ǣ�������| A�� | a��b��c | B�� | a=b=c | C�� | c��a��b | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ�����}
| �\(y��n)ݔ���� | ;��ƽ���ٶȣ�ǧ��/�r(sh��)�� | �\(y��n)�M(f��i)��Ԫ/ǧ�ף� | �bж�M(f��i)�ã�Ԫ�� |
| ��܇ | 100 | 15 | 2000 |
| ��܇ | 80 | 20 | 900 |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ��x���}
| A�� | ���(xi��ng)ʽ$\frac{1}{2}$xy��ϵ��(sh��)��$\frac{1}{2}$���Δ�(sh��)��1 | |
| B�� | ���(xi��ng)ʽ-$\frac{1}{3}$��a2b3��ϵ��(sh��)��-$\frac{1}{3}$���Δ�(sh��)��6 | |
| C�� | ���(xi��ng)ʽx2��ϵ��(sh��)��1���Δ�(sh��)��2 | |
| D�� | ���(xi��ng)ʽ2x3-3x2y2+x-1���������(xi��ng)ʽ |
�鿴�𰸺ͽ���>>
��Ŀ�����Д�(sh��)�W(xu��) ��(l��i)Դ�� �}�ͣ��x���}
| A�� |  | B�� | 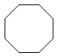 | C�� |  | D�� | 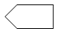 |
�鿴�𰸺ͽ���>>
�ٶ����� - ����(x��)��(c��)�б� - ԇ�}�б�
����ʡ��(li��n)�W(w��ng)�`���Ͳ�����Ϣ�e��(b��o)ƽ�_(t��i) | �W(w��ng)���к���Ϣ�e��(b��o)���^(q��) | ����p�_�e��(b��o)���^(q��) | ��vʷ̓�o(w��)���x�к���Ϣ�e��(b��o)���^(q��) | �����֙�(qu��n)�e��(b��o)���^(q��)
�`���Ͳ�����Ϣ�e��(b��o)�Ԓ��027-86699610 �e��(b��o)�]�䣺58377363@163.com