
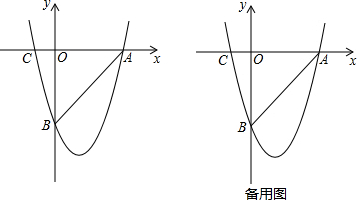
 如圖,拋物線y=-x2+2x+3與x軸交于A、B兩點(diǎn),與y軸交于點(diǎn)C,D為拋物線的頂點(diǎn).
如圖,拋物線y=-x2+2x+3與x軸交于A、B兩點(diǎn),與y軸交于點(diǎn)C,D為拋物線的頂點(diǎn).分析 (1)先根據(jù)拋物線y=-x2+2x+3求出拋物線與x軸交點(diǎn)A、B兩點(diǎn)坐標(biāo),與y軸交點(diǎn)C,以及拋物線的頂點(diǎn)D的坐標(biāo),再根據(jù)直角坐標(biāo)系中兩點(diǎn)間距離公式求出△BCD三邊的長(zhǎng)度,再根據(jù)勾股定理的逆定理判定△BCD是直角三角形,從而求出∠BCD=90°;
(2)根據(jù)點(diǎn)P為拋物線上一動(dòng)點(diǎn),且△PAC是直角三角形,分情況討論:①∠PCA=90°,根據(jù)直角坐標(biāo)系中兩直線垂直其斜率(k值)互為負(fù)倒數(shù),先求出直線PC的解析式為y=-$\frac{1}{3}$x+3,再利用解析式聯(lián)立方程組求交點(diǎn)坐標(biāo)的方法求出點(diǎn)P坐標(biāo);②∠PAC=90°,方法同①;③根據(jù)題意可知∠APC≠90°.故點(diǎn)P的坐標(biāo)有兩種情況:($\frac{7}{3}$,$\frac{20}{9}$)或($\frac{10}{3}$,$-\frac{13}{9}$).
解答 解:(1)當(dāng)y=0時(shí),-x2+2x+3=0,解得x1=-1,x2=3,即A(-1,0);B(3,0);
當(dāng)x=0時(shí),y=3,即C(0,3);
拋物線y=-x2+2x+3的頂點(diǎn)坐標(biāo)為D(1,4);
∵DC=$\sqrt{(1-0)^{2}+(4-3)^{2}}$=$\sqrt{2}$
BC=$\sqrt{(3-0)^{2}+(0-3)^{2}}$=$\sqrt{18}$
BD=$\sqrt{(3-1)^{2}+(0-4)^{2}}$=$\sqrt{20}$
∴DC2+BC2=BD2
∴∠BCD=90°;
(2)設(shè)直線AC的解析式為y=kx+b,把點(diǎn)A,C代入得
$\left\{\begin{array}{l}{-k+b=0}\\{b=3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=3}\\{b=3}\end{array}\right.$.
故直線AC的解析式為:y=3x+3
①若∠PCA=90°,則PC⊥AC,所以直線PC的解析式為:y=-$\frac{1}{3}$x+3,
y=-$\frac{1}{3}$x+3與y=-x2+2x+3聯(lián)立方程組得$\left\{\begin{array}{l}{y=-\frac{1}{3}x+3}\\{y=-{x}^{2}+2x+3}\end{array}\right.$
解得:$\left\{\begin{array}{l}{{x}_{1}=0}\\{{y}_{1}=3}\end{array}\right.$ (舍去),$\left\{\begin{array}{l}{{x}_{2}=\frac{7}{3}}\\{{y}_{2}=\frac{20}{9}}\end{array}\right.$
∴P($\frac{7}{3}$,$\frac{20}{9}$)
②若∠PAC=90°,則PA⊥AC,所以直線PA的解析式為:y=-$\frac{1}{3}$x+n
把點(diǎn)A(-1,0)代入得n=-$\frac{1}{3}$.
故y=-$\frac{1}{3}$x$-\frac{1}{3}$
y=-$\frac{1}{3}$x$-\frac{1}{3}$與y=-x2+2x+3聯(lián)立方程組得
$\left\{\begin{array}{l}{y=-\frac{1}{3}x-\frac{1}{3}}\\{y=-{x}^{2}+2x+3}\end{array}\right.$,
解得$\left\{\begin{array}{l}{{x}_{1}=-1}\\{{y}_{1}=0}\end{array}\right.$ (舍去),$\left\{\begin{array}{l}{{x}_{2}=\frac{10}{3}}\\{{y}_{2}=-\frac{13}{9}}\end{array}\right.$
故P($\frac{10}{3}$,$-\frac{13}{9}$)
③根據(jù)題意可知∠APC≠90°.
綜上可知點(diǎn)P的坐標(biāo)為($\frac{7}{3}$,$\frac{20}{9}$)或($\frac{10}{3}$,$-\frac{13}{9}$).
點(diǎn)評(píng) 本題主要考查了二次函數(shù)的圖象上一些特殊點(diǎn)的求法即應(yīng)用.第(1)問(wèn)根據(jù)直角坐標(biāo)系中兩點(diǎn)間距離公式AB=$\sqrt{({x}_{1}-{x}_{2})^{2}+({y}_{1}-{y}_{2})^{2}}$求線段的長(zhǎng)度,再利用勾股定理的逆定理判定直角三角形是解決此類問(wèn)題的關(guān)鍵;第(2)問(wèn)根據(jù)直角三角形的性質(zhì)求動(dòng)點(diǎn)坐標(biāo),若題目中沒(méi)有給定直角應(yīng)該分情況討論.利用直角坐標(biāo)系中兩直線垂直其斜率(k值)互為負(fù)倒數(shù)的方法求直線解析式的方法要掌握,可以簡(jiǎn)化計(jì)算.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 如圖,矩形網(wǎng)格由小正方形構(gòu)成,每一個(gè)小正方形的邊長(zhǎng)都為1,點(diǎn)A和點(diǎn)B是小正方形的頂點(diǎn),則點(diǎn)A和點(diǎn)B之間的距離為5.
如圖,矩形網(wǎng)格由小正方形構(gòu)成,每一個(gè)小正方形的邊長(zhǎng)都為1,點(diǎn)A和點(diǎn)B是小正方形的頂點(diǎn),則點(diǎn)A和點(diǎn)B之間的距離為5.查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題

查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:解答題
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
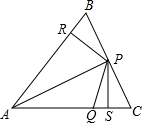 如圖,△ABC中,P、Q分別是BC、AC上的點(diǎn),作PR⊥AB,PS⊥AC,垂足分別是R、S,若AQ=PQ,PR=PS,下面四個(gè)結(jié)論:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正確結(jié)論的序號(hào)是①②④(請(qǐng)將所有正確結(jié)論的序號(hào)都填上).
如圖,△ABC中,P、Q分別是BC、AC上的點(diǎn),作PR⊥AB,PS⊥AC,垂足分別是R、S,若AQ=PQ,PR=PS,下面四個(gè)結(jié)論:①AS=AR;②QP∥AR;③△BRP≌△QSP;④AP垂直平分RS.其中正確結(jié)論的序號(hào)是①②④(請(qǐng)將所有正確結(jié)論的序號(hào)都填上).查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:填空題
 頤和園是我國(guó)現(xiàn)存規(guī)模最大,保存最完整的古代皇家園林,它和承德避暑山莊、蘇州拙政園、蘇州留園并稱為中國(guó)四大名園.該園有一個(gè)六角亭,如果它的地基是半徑為2米的正六邊形,那么這個(gè)地基的周長(zhǎng)是12米.
頤和園是我國(guó)現(xiàn)存規(guī)模最大,保存最完整的古代皇家園林,它和承德避暑山莊、蘇州拙政園、蘇州留園并稱為中國(guó)四大名園.該園有一個(gè)六角亭,如果它的地基是半徑為2米的正六邊形,那么這個(gè)地基的周長(zhǎng)是12米.查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com