
分析 分兩種情況討論:①點P的路徑是一段弧,由題目不難看出當D為AC的中點的時候,點P經(jīng)過弧AB的中點,此時△ABP為等腰三角形,繼而求得半徑和對應(yīng)的圓心角的度數(shù),求得答案.②點E靠近點B時,點P的路徑就是過點C向AB做的垂線段.
解答 解:若AE=BD,則有AD=BE或AD=CE兩種情況:
①當AD=CE時,點P的路徑是一段弧,當D為AC的中點的時候,點P經(jīng)過弧AB的中點,
此時△ABP為等腰三角形,且∠ABP=∠BAP=30°,
∴∠AOB=120°,
又∵AB=18,
∴OA=6$\sqrt{3}$,
∴點P的路徑長l=$\frac{120×π×6\sqrt{3}}{180}$=4$\sqrt{3}$π;
②當AD=BE時,點P的路徑就是過點C向AB作的垂線段CG,
因為等邊三角形ABC的邊長為18,
所以點P的路徑長CG為:9$\sqrt{3}$.
故答案為:4$\sqrt{3}$π或9$\sqrt{3}$.
點評 本題考查了等邊三角形的性質(zhì)的運用,全等三角形的判定及性質(zhì)的運用,弧線長公式的運用,解答時證明三角形全等是關(guān)鍵,解答本題時注意轉(zhuǎn)化思想的運用.


科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
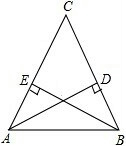 如圖,從C地看A,B兩地的視角∠C是銳角,從C地到A,B兩地的距離相等,A地到路段BC的距離AD與B地到路段AC的距離BE相等嗎?為什么?
如圖,從C地看A,B兩地的視角∠C是銳角,從C地到A,B兩地的距離相等,A地到路段BC的距離AD與B地到路段AC的距離BE相等嗎?為什么?查看答案和解析>>
科目:初中數(shù)學 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
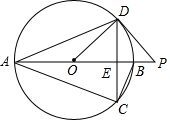 已知:如圖,AB是⊙O的直徑,CD是弦,且AB⊥CD于E,P是AB延長線上一點,連接PD,∠PDC=∠CAD.
已知:如圖,AB是⊙O的直徑,CD是弦,且AB⊥CD于E,P是AB延長線上一點,連接PD,∠PDC=∠CAD.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
 如圖,已知一次函數(shù)y=mx的圖象經(jīng)過點A(-2,4),點A關(guān)于y軸的對稱點B在反比例函數(shù)y=$\frac{k}{x}$的圖象上.
如圖,已知一次函數(shù)y=mx的圖象經(jīng)過點A(-2,4),點A關(guān)于y軸的對稱點B在反比例函數(shù)y=$\frac{k}{x}$的圖象上.查看答案和解析>>
科目:初中數(shù)學 來源: 題型:選擇題
| A. | $\frac{AB}{DE}$=$\frac{AC}{DF}$ | B. | $\frac{AB}{DE}$=$\frac{BC}{EF}$ | C. | ∠A=∠E | D. | ∠B=∠D |
查看答案和解析>>
科目:初中數(shù)學 來源: 題型:解答題
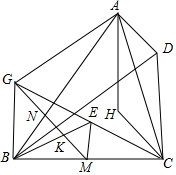 如圖,已知H為銳角△ABC的垂心,D是使四邊形AHCD為平行四邊形的一點,過BC的中點M作AB的垂線,垂足為N,K為MN的中點,過點A作BD的平行線交MN于點G,若A,K,M,C四點共圓.求證:直線BK平分線段CG.
如圖,已知H為銳角△ABC的垂心,D是使四邊形AHCD為平行四邊形的一點,過BC的中點M作AB的垂線,垂足為N,K為MN的中點,過點A作BD的平行線交MN于點G,若A,K,M,C四點共圓.求證:直線BK平分線段CG.查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com