
 已知數軸上兩點A、B對應的數分別為-1、3,點P為數軸上一動點,其對應的數為x.
已知數軸上兩點A、B對應的數分別為-1、3,點P為數軸上一動點,其對應的數為x.分析 (1)由點P到點A,點B的距離相等,可知點P位于線段AB的中點處,從而可以得到點P對應的數;
(2)由數軸可知點A對應的數為-1,點B對應的數為3,3-(-1)=4,又因為數軸上,點P到點A、點B的距離之和為5,可知點P位于點A的左側或點B的右側,本題得以解決;
(3)根據點P以每秒1個單位長度的速度從原點O向左運動,同時點B以每秒3個單位長度的速度沿數軸向左運動(點A保持不動),當點P到點A、點B的距離相等時,此時點P位于線段AB的中點處或點B與點A重合,從而可以得到點P對應的數,從而可得到運動時間t的值.
解答 解:(1)∵數軸上兩點A、B對應的數分別為-1、3,
∴點P到點A,點B的距離相等,點P對應的數是:$\frac{-1+3}{2}=1$.
故答案為:1;
(2)∵數軸上兩點A、B對應的數分別為-1、3,
∴點A、B之間的距離是:3-(-1)=4,
∵4<5,
∴點P到點A、點B的距離之和為5時,點P位于點A的左側或位于點B的右側,
∴當點P位于點A的左側時,3-x+(-1)-x=5,解得x=-1.5,
當點P位于點B的右側時,x-3+x-(-1)=5,解得x=3.5.
故答案為:-1.5或3.5;
(3)∵點P以每秒1個單位長度的速度從原點O向左運動,同時點B以每秒3個單位長度的速度沿數軸向左運動(點A保持不動),
∴點P到點A、點B的距離相等時,點P位于線段AB的中點處或點B與點A重合,
∴當點P位于線段AB的中點處時,$\frac{3-3t+-1}{2}=-t$,解得t=2,
當點A與點B重合時,3-3t=-1,解得t=$\frac{4}{3}$,
即當點P以每秒1個單位長度的速度從原點O向左運動,同時點B以每秒3個單位長度的速度沿數軸向左運動(點A保持不動),當點P到點A、點B的距離相等時,運動時間t的值是2或$\frac{4}{3}$.
點評 本題考查一元一次方程的應用和數軸,解題的關鍵是明確題意,找出所求問題需要的條件.


 優等生題庫系列答案
優等生題庫系列答案 53天天練系列答案
53天天練系列答案科目:初中數學 來源: 題型:填空題
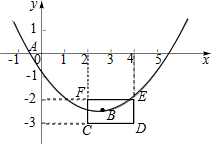 如圖,拋物線y=ax2+bx+c與x軸的一個交點A在點(-1,0)和(0,0)之間(包括這兩點),頂點B是矩形CDEF上(包括邊界和內部)的一個動點,則a的取值范圍是$\frac{2}{25}$≤a≤$\frac{3}{4}$.
如圖,拋物線y=ax2+bx+c與x軸的一個交點A在點(-1,0)和(0,0)之間(包括這兩點),頂點B是矩形CDEF上(包括邊界和內部)的一個動點,則a的取值范圍是$\frac{2}{25}$≤a≤$\frac{3}{4}$.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
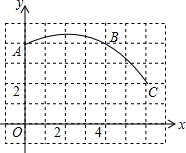 如圖,在單位長度為1的正方形網格中建立一直角坐標系,一條圓弧經過網格點A、B、C,請在網格圖中進行下列操作:
如圖,在單位長度為1的正方形網格中建立一直角坐標系,一條圓弧經過網格點A、B、C,請在網格圖中進行下列操作:查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com