
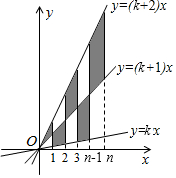
 在x正半軸上有n個連續整數點,它們的橫坐標依次為1,2,3,…,n,分別過這些點作x軸的垂線與三條直線y=kx,y=(k+1)x,y=(k+2)x相交,其中k>0,則圖中陰影部分的面積總和是$\frac{1}{2}$n2.
在x正半軸上有n個連續整數點,它們的橫坐標依次為1,2,3,…,n,分別過這些點作x軸的垂線與三條直線y=kx,y=(k+1)x,y=(k+2)x相交,其中k>0,則圖中陰影部分的面積總和是$\frac{1}{2}$n2. 分析 分別把x=1,x=2,x=3,…,x=n代入解析式,求出梯形或三角形的邊長,根據面積公式求出即可
解答 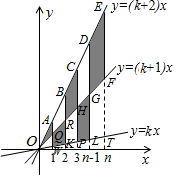 解:把x=1分別代入y=kx,y=(k+1)x,y=(k+2)x得:AW=k+2,WQ=k+1-k=1,
解:把x=1分別代入y=kx,y=(k+1)x,y=(k+2)x得:AW=k+2,WQ=k+1-k=1,
∴AQ=k+2-(k+1)=1,
同理:BR=RK=2,CH=HP=3,DG=GL=4,EF=FT=5,
2-1=1,3-2=1,4-3=1,5-4=1,
∴圖中陰影部分的面積是$\frac{1}{2}$×1×1+$\frac{1}{2}$×(1+2)×1+$\frac{1}{2}$×(2+3)×1+…+$\frac{1}{2}$×(n-2+n-1)×1+$\frac{1}{2}$×(n-1+n)×1=$\frac{1}{2}$n2.
故答案為:$\frac{1}{2}$n2.
點評 此題主要考查了一次函數和三角形的面積公式,要會根據點的坐標求出所需要的線段的長度,靈活運用面積公式求解.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:填空題
 如圖,△DEF的邊長分別為1,$\sqrt{3}$,2,正六邊形網格是由24個邊長為2的正三角形組成,選擇格點為頂點畫△ABC,使得△ABC∽△DEF.如果相似比$\frac{AB}{DE}$=k,那么k的值可以是2,2$\sqrt{3}$,4.
如圖,△DEF的邊長分別為1,$\sqrt{3}$,2,正六邊形網格是由24個邊長為2的正三角形組成,選擇格點為頂點畫△ABC,使得△ABC∽△DEF.如果相似比$\frac{AB}{DE}$=k,那么k的值可以是2,2$\sqrt{3}$,4.查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. | 函數值隨自變量的增大而減小 | |
| B. | 函數的圖象不經過第三象限 | |
| C. | 函數的圖象與x軸的交點坐標是(0,4) | |
| D. | 函數的圖象向下平移4個單位長度得y=-2x的圖象 |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
 風車不能做成軸對稱圖形,應做成中心對稱圖形才能在風口處平穩旋轉,如圖,現有一長條矩形硬紙板(其中心有一個小孔)和兩張全等的矩形薄紙片,將紙片粘到硬紙板上,做成一個能繞著小孔平穩旋轉的風車,正確的粘合方法是( )
風車不能做成軸對稱圖形,應做成中心對稱圖形才能在風口處平穩旋轉,如圖,現有一長條矩形硬紙板(其中心有一個小孔)和兩張全等的矩形薄紙片,將紙片粘到硬紙板上,做成一個能繞著小孔平穩旋轉的風車,正確的粘合方法是( )| A. | 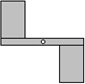 | B. | 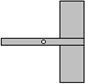 | C. |  | D. |  |
查看答案和解析>>
科目:初中數學 來源: 題型:選擇題
| A. |  | B. |  | C. |  | D. |  |
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com