
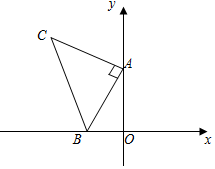
 如圖,平面直角坐標系中有點B(-1,0)和y軸上一動點A(0,a),其中a>0,以A點為直角頂點在第二象限內作等腰直角△ABC,設點C的坐標為(c,d).
如圖,平面直角坐標系中有點B(-1,0)和y軸上一動點A(0,a),其中a>0,以A點為直角頂點在第二象限內作等腰直角△ABC,設點C的坐標為(c,d).分析 (1)先過點C作CE⊥y軸于E,證△AEC≌△BOA,推出CE=OA=2,AE=BO=1,即可得出點C的坐標;
(2)先過點C作CE⊥y軸于E,證△AEC≌△BOA,推出CE=OA=a,AE=BO=1,可得OE=a=1,即可得出點C的坐標為(-a,a+1),據此可得c+d的值不變;
(3)分為三種情況討論,分別畫出符合條件的圖形,構造直角三角形,證出三角形全等,根據全等三角形對應邊相等即可得出答案;
解答  解:(1)如圖,過點C作CE⊥y軸于E,則∠CEA=∠AOB,
解:(1)如圖,過點C作CE⊥y軸于E,則∠CEA=∠AOB,
∵△ABC是等腰直角三角形,
∴AC=BA,∠BAC=90°,
∴∠ACE+∠CAE=90°=∠BAO+∠CAE,
∴∠ACE=∠BAO,
在△ACE和△BAO中,
$\left\{\begin{array}{l}{∠CEA=∠AOB}\\{∠ACE=∠BAO}\\{AC=BA}\end{array}\right.$,
∴△ACE≌△BAO(AAS),
∵B(-1,0),A(0,2),
∴BO=AE=1,AO=CE=2,
∴OE=1+2=3,
∴C(-2,3),
故答案為:-2,3;
(2)動點A在運動的過程中,c+d的值不變.
過點C作CE⊥y軸于E,則∠CEA=∠AOB,
∵△ABC是等腰直角三角形,
∴AC=BA,∠BAC=90°,
∴∠ACE+∠CAE=90°=∠BAO+∠CAE,
∴∠ACE=∠BAO,
在△ACE和△BAO中,
$\left\{\begin{array}{l}{∠CEA=∠AOB}\\{∠ACE=∠BAO}\\{AC=BA}\end{array}\right.$,
∴△ACE≌△BAO(AAS),
∵B(-1,0),A(0,a),
∴BO=AE=1,AO=CE=a,
∴OE=1+a,
∴C(-a,1+a),
又∵點C的坐標為(c,d),
∴c+d=-a+1+a=1,即c+d的值不變;
(3)存在一點P,使△PAB與△ABC全等,
分為三種情況:
①如圖,過P作PE⊥x軸于E,則∠PBA=∠AOB=∠PEB=90°,
∴∠EPB+∠PBE=90°,∠PBE+∠ABO=90°,
∴∠EPB=∠ABO,
在△PEB和△BOA中,
$\left\{\begin{array}{l}{∠EPB=∠ABO}\\{∠PEB=∠BOA}\\{PB=BA}\end{array}\right.$,
∴△PEB≌△BOA(AAS),
∴PE=BO=1,EB=AO=2,
∴OE=2+1=3,
即P的坐標是(-3,1);
②如圖,過C作CM⊥x軸于M,過P作PE⊥x軸于E, 則∠CMB=∠PEB=90°,
則∠CMB=∠PEB=90°,
∵△CAB≌△PAB,
∴∠PBA=∠CBA=45°,BC=BP,
∴∠CBP=90°,
∴∠MCB+∠CBM=90°,∠CBM+∠PBE=90°,
∴∠MCB=∠PBE,
在△CMB和△BEP中,
$\left\{\begin{array}{l}{∠MCB=∠PBE}\\{∠CMB=∠PEB}\\{BC=BP}\end{array}\right.$,
∴△CMB≌△BEP(AAS),
∴PE=BM,CM=BE,
∵C(-2,3),B(-1,0),
∴PE=1,OE=BE-BO=3-1=2,
即P的坐標是(2,1);
③如圖,過P作PE⊥x軸于E, 則∠BEP=∠BOA=90°,
則∠BEP=∠BOA=90°,
∵△CAB≌△PBA,
∴AB=BP,∠CAB=∠ABP=90°,
∴∠ABO+∠PBE=90°,∠PBE+∠BPE=90°,
∴∠ABO=∠BPE,
在△BOA和△PEB中,
$\left\{\begin{array}{l}{∠ABO=∠BBPE}\\{∠BOA=∠PEB}\\{BA=BP}\end{array}\right.$,
∴△BOA≌△PEB(AAS),
∴PE=BO=1,BE=OA=2,
∴OE=BE-BO=2-1=1,
即P的坐標是(1,-1),
綜合上述,符合條件的P的坐標是(-3,1)或(2,1)或(1,-1).
點評 本題屬于三角形綜合題,主要考查了全等三角形的性質和判定,三角形內角和定理,等腰直角三角形性質的應用,考核了學生綜合運用性質進行推理的能力,解決問題的關鍵是作輔助線構造全等三角形以及運用運用分類討論的思想.


科目:初中數學 來源: 題型:解答題
| 累計購物 實際花費 | 500 | 700 | … | x |
| 在甲商場 | 400 | 560 | … | 0.8x |
| 在乙商場 | 410 | 550 | … | 0.7x+60 |
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題


查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com