

分析 (1)①把M點(diǎn)坐標(biāo)代入可求得m的值,可求m的值,可求反比例函數(shù)解析式;②由反比例函數(shù)解析式可求得N點(diǎn)坐標(biāo),結(jié)合函數(shù)圖象可求得答案;
(2)由M、N的坐標(biāo),利用待定系數(shù)法可求得直線MN的解析式,再求得平移后直線解析式,聯(lián)立直線和反比例函數(shù)解析式,消去y可得到一元二次方程,由條件可知其判別式為0,可求得a的值;
(3)過C作CD⊥y軸于點(diǎn)D,由條件可得OB=OD,OA=$\frac{1}{2}$CD,再結(jié)合反比例函數(shù)解析式可求得OD•CD,則可求得OA•OB.
解答 解:
(1)①∵反比例函數(shù)y2=$\frac{m}{x}$(m為常數(shù),m≠0)的圖象過點(diǎn)M(1,4),
∴m=1×4=4,
∴反比例函數(shù)解析式為y=$\frac{4}{x}$,
故答案為:y=$\frac{4}{x}$;
②∵M(jìn)、N橫坐標(biāo)分別為x=1和x=4,
∴當(dāng)y1≤y2時,即直線MN在反比例函數(shù)下方時對應(yīng)的x的取值范圍,
∴x≤1或x≥4,
故答案為:x≤1或x≥4;
(2)∵反比例函數(shù)y=$\frac{4}{x}$的圖象過點(diǎn)N(4,n),
∴4n=4,解得n=1,
∴N(4,1),
設(shè)直線MN解析式為y=kx+b,
∴$\left\{\begin{array}{l}{k+b=4}\\{4k+b=1}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=-1}\\{b=5}\end{array}\right.$,
∴直線MN解析式為y=-x+5,
把直線MN向下平移a個單位其解析式為y=-x+5-a,
聯(lián)立直線和反比例函數(shù)解析式,消去y可得-x+5-a=$\frac{4}{x}$,
整理可得x2+(a-5)x+4=0,
∵直線MN向下平移后與反比例函數(shù)的圖象有且只有一個公共點(diǎn),
∴方程x2+(a-5)x+4=0有兩個相等的實(shí)數(shù)根,
∴△=0,即(a-5)2-16=0,
解得a=9或a=1;
(3)如圖,過C作CD⊥y軸于點(diǎn)D,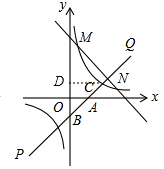
∵BC=2AC,
∴A為BC中點(diǎn),
∵CD∥OA,
∴O為BD中點(diǎn),
∴OB=OD,OA=$\frac{1}{2}$CD,
∵點(diǎn)C在反比例函數(shù)y=$\frac{4}{x}$的圖象上,
∴OA•OB=$\frac{1}{2}$CD•OD=$\frac{1}{2}$×4=2.
點(diǎn)評 本題為反比例函數(shù)的綜合應(yīng)用,涉及函數(shù)圖象的交點(diǎn)、待定系數(shù)法、圖象的平移、三角形中位線定理、一元二次方程根的判別式及數(shù)形結(jié)合思想等知識.在(1)中注意兩函數(shù)圖象的交點(diǎn)坐標(biāo)滿足每個函數(shù)解析式,在(2)中由條件得到關(guān)于a的方程是解題的關(guān)鍵,在(3)中用C點(diǎn)的坐標(biāo)表示出OA和OB是解題的關(guān)鍵.本題考查知識點(diǎn)較多,綜合性較強(qiáng),難度適中.



| 年級 | 高中課程 | 年級 | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 不變 | B. | 擴(kuò)大到原來的2倍 | C. | 縮小到原來的$\frac{1}{2}$ | D. | 縮小到原來的$\frac{1}{4}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
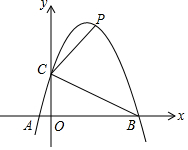 已知拋物線y=ax2-2ax+m與x軸交于A(-1,0)、B(x2,0)兩點(diǎn),與y軸正半軸交于點(diǎn)C,且滿足S△ABC=4.
已知拋物線y=ax2-2ax+m與x軸交于A(-1,0)、B(x2,0)兩點(diǎn),與y軸正半軸交于點(diǎn)C,且滿足S△ABC=4.查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | (2,1) | B. | (2,-1) | C. | (1,-2) | D. | (0,5) |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
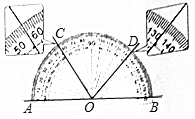 已知直線AB,射線OC,OD都在如圖所示的量角器上,點(diǎn)O在直線AB上,則下列判斷中不正確的是( )
已知直線AB,射線OC,OD都在如圖所示的量角器上,點(diǎn)O在直線AB上,則下列判斷中不正確的是( )| A. | ∠AOC=56° | B. | ∠AOD=134° | C. | ∠AOC<∠COD | D. | ∠BOD與∠BOC互補(bǔ) |
查看答案和解析>>
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺 | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com