
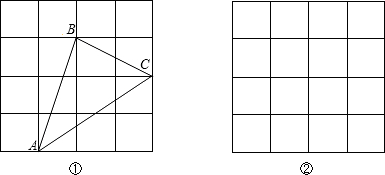
分析 (1)根據(jù)AB=$\sqrt{10}$,BC=$\sqrt{5}$,AC=$\sqrt{13}$,可得AB2+BC2≠AC2,即可得出△ABC不是直角三角形;
(2)根據(jù)△DEF為鈍角三角形,且面積為4進(jìn)行作圖即可.
解答 解:(1)如圖1,∵AB=$\sqrt{10}$,BC=$\sqrt{5}$,AC=$\sqrt{13}$,
∴AB2+BC2≠AC2,
∴△ABC不是直角三角形;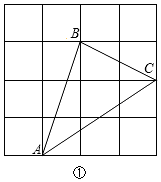
故答案為:不是;
(2)如圖2,△DEF中∠DEF>90°,△DEF的面積=$\frac{1}{2}$×2×4=4.
∴△DEF即為所求.
點(diǎn)評(píng) 本題主要考查了復(fù)雜作圖以及三角形面積的計(jì)算,解決問題的關(guān)鍵是掌握勾股定理的逆定理.如果三角形的三邊長(zhǎng)a,b,c滿足a2+b2=c2,那么這個(gè)三角形就是直角三角形.


 閱讀快車系列答案
閱讀快車系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:解答題
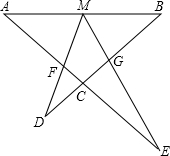 如圖,AE與BD交于點(diǎn)C,∠DME=∠A=∠B,且DM交AC于F,ME交BC于G
如圖,AE與BD交于點(diǎn)C,∠DME=∠A=∠B,且DM交AC于F,ME交BC于G查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
 如圖,A,B兩點(diǎn)在數(shù)軸上,點(diǎn)A表示的數(shù)為-10,OB=4OA,點(diǎn)M以每秒2個(gè)單位長(zhǎng)度的速度從點(diǎn)A開始向左運(yùn)動(dòng),點(diǎn)N以每秒3個(gè)單位長(zhǎng)度的速度從點(diǎn)B開始向左運(yùn)動(dòng)(點(diǎn)M和點(diǎn)N同時(shí)出發(fā))
如圖,A,B兩點(diǎn)在數(shù)軸上,點(diǎn)A表示的數(shù)為-10,OB=4OA,點(diǎn)M以每秒2個(gè)單位長(zhǎng)度的速度從點(diǎn)A開始向左運(yùn)動(dòng),點(diǎn)N以每秒3個(gè)單位長(zhǎng)度的速度從點(diǎn)B開始向左運(yùn)動(dòng)(點(diǎn)M和點(diǎn)N同時(shí)出發(fā))查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:選擇題
| A. | 2 | B. | $\frac{3}{2}$ | C. | $\frac{1}{2}$ | D. | $-\frac{1}{3}$ |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:填空題
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
| 購物金額(原價(jià)) | 優(yōu)惠率 |
| 不超過3000元的部分 | 無優(yōu)惠 |
| 超過3000元但不超過10000元部分 | 5% |
| 超過10000元的部分 | 10% |
| 付款時(shí),還可以享受單筆消費(fèi)滿2000元立減160元優(yōu)惠 | |
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:解答題
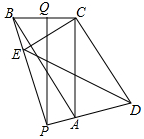 如圖,在△ABC中,∠ACB=90°,BC=6,AC=8,將△ABC繞C點(diǎn)旋轉(zhuǎn)一個(gè)角度到△DEC,直線AD,EB交于P點(diǎn),Q是BC的中點(diǎn),連PQ,在旋轉(zhuǎn)過程中,求:
如圖,在△ABC中,∠ACB=90°,BC=6,AC=8,將△ABC繞C點(diǎn)旋轉(zhuǎn)一個(gè)角度到△DEC,直線AD,EB交于P點(diǎn),Q是BC的中點(diǎn),連PQ,在旋轉(zhuǎn)過程中,求:查看答案和解析>>
百度致信 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com