
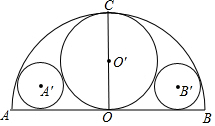
 已知:如圖,以AB為直徑作半圓,半徑OC⊥AB,以OC為直徑作⊙OO′,再作⊙A′和⊙B都與AB、⊙O及⊙O′相切,如果AB=2R,求⊙A′的半徑.
已知:如圖,以AB為直徑作半圓,半徑OC⊥AB,以OC為直徑作⊙OO′,再作⊙A′和⊙B都與AB、⊙O及⊙O′相切,如果AB=2R,求⊙A′的半徑. 分析 連接OA′并延長交⊙O于D,作A′E⊥AB于E,A′F⊥OC于F,連接A′O′,如圖,設⊙A′的半徑為r,利用切線的性質和相切兩圓的連心線過切點得到OC=OD=R,A′D=A′E=r,A′O′=r+$\frac{R}{2}$,再證明四邊形A′EOF為矩形得到OF=A′E=r,則O′F=O′O-OF=$\frac{R}{2}$-r,接著利用勾股定理建立方程得到(R-r)2-r2=($\frac{1}{2}$R+r)2-($\frac{1}{2}$R-r)2,然后解關于r的一元二次方程即可.
解答 解:連接OA′并延長交⊙O于D,作A′E⊥AB于E,A′F⊥OC于F,連接A′O′,如圖,設⊙A′的半徑為r,
∵⊙A′和⊙B都與AB、⊙O及⊙O′相切,
∴OC=OD=R,A′D=A′E=r,A′O′=r+$\frac{R}{2}$,
∵OC⊥AB,A′E⊥AB,A′F⊥OC,
∴四邊形A′EOF為矩形,
∴OF=A′E=r,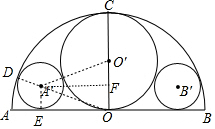
∴O′F=O′O-OF=$\frac{R}{2}$-r,
在Rt△A′OF中,A′F2=OA′2-OF2=(R-r)2-r2,
在Rt△A′O′F中,A′F2=O′A′2-O′F2=($\frac{1}{2}$R+r)2-($\frac{1}{2}$R-r)2,
∴(R-r)2-r2=($\frac{1}{2}$R+r)2-($\frac{1}{2}$R-r)2,
整理得r2-3Rr+R2=0,解得r1=$\frac{3-\sqrt{5}}{2}$R,r2=$\frac{3+\sqrt{5}}{2}$R(舍去),
∴⊙A′的半徑為$\frac{3-\sqrt{5}}{2}$R.
點評 本題考查了切線的性質:圓的切線垂直于經過切點的半徑.若出現圓的切線,必連過切點的半徑,構造定理圖,得出垂直關系.也考查了兩圓相切的性質和勾股定理.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:解答題

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 (1)用適當的方法解下列一元二次方程:x2-6x+1=0.
(1)用適當的方法解下列一元二次方程:x2-6x+1=0.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
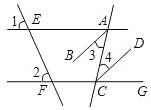 如圖,直線AE、CF分別被直線EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.將下列證明AB∥CD的過程及理由填寫完整.
如圖,直線AE、CF分別被直線EF、AC所截,已知,∠1=∠2,AB平分∠EAC,CD平分∠ACG.將下列證明AB∥CD的過程及理由填寫完整.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
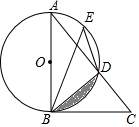 如圖所示,AB是⊙O的直徑,BC與⊙O相切,切點為B,AC與⊙O相交于點D,點E是$\widehat{AD}$上任一點.
如圖所示,AB是⊙O的直徑,BC與⊙O相切,切點為B,AC與⊙O相交于點D,點E是$\widehat{AD}$上任一點.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
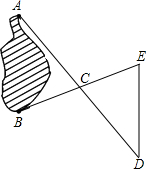 如圖,A、B兩點分別位于一個池塘的兩端.小明想用繩子測量A、B間的距離,但繩子不夠長,小明想出了這樣一個辦法:先在地上取一個可以直接到達A點和B點的點C,連接AC并延長到D,使CD=AC;連接BC并延長到E,使CE=CB,連接DE并測量出它的長度,DE的長度就是A、B間的距離.請你說明其中的道理.
如圖,A、B兩點分別位于一個池塘的兩端.小明想用繩子測量A、B間的距離,但繩子不夠長,小明想出了這樣一個辦法:先在地上取一個可以直接到達A點和B點的點C,連接AC并延長到D,使CD=AC;連接BC并延長到E,使CE=CB,連接DE并測量出它的長度,DE的長度就是A、B間的距離.請你說明其中的道理.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com