Question

7．（1）如圖1，O是等邊△ABC內一點，連接OA、OB、OC，且OA=3，OB=4，OC=5，將△BAO繞點B順時針旋轉后得到△BCD，連接OD．求：
①旋轉角的度數(shù)；
②線段OD的長；
③∠BDC的度數(shù)．
（2）如圖2所示，O是等腰直角△ABC（∠ABC=90°）內一點，連接OA、OB、OC，將△BAO繞點B順時針旋轉后得到△BCD，連接OD．當OA、OB、OC滿足什么條件時，∠ODC=90°？請給出證明．

Answer 1

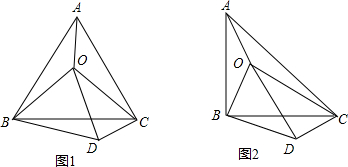
分析 （1）①根據(jù)等邊三角形的性質得BA=BC，∠ABC=60°，再根據(jù)旋轉的性質得∠OBD=∠ABC=60°，于是可確定旋轉角的度數(shù)為60°；
②由旋轉的性質得BO=BD，加上∠OBD=60°，則可判斷△OBD為等邊三角形，所以OD=OB=4；
③由△BOD為等邊三角形得到∠BDO=60°，再利用旋轉的性質得CD=AO=3，然后根據(jù)勾股定理的逆定理可證明△OCD為直角三角形，∠ODC=90°，所以∠BDC=∠BDO+∠ODC=150°；
（2）根據(jù)旋轉的性質得∠OBD=∠ABC=90°，BO=BD，CD=AO，則可判斷△OBD為等腰直角三角形，則OD=$\sqrt{2}$OB，然后根據(jù)勾股定理的逆定理，當CD²+OD²=OC²時，△OCD為直角三角形，∠ODC=90°．

解答 解：（1）①∵△ABC為等邊三角形，
∴BA=BC，∠ABC=60°，
∵△BAO繞點B順時針旋轉后得到△BCD，
∴∠OBD=∠ABC=60°，
∴旋轉角的度數(shù)為60°；
②∵△BAO繞點B順時針旋轉后得到△BCD，
∴BO=BD，
而∠OBD=60°，
∴△OBD為等邊三角形；
∴OD=OB=4；
③∵△BOD為等邊三角形，
∴∠BDO=60°，
∵△BAO繞點B順時針旋轉后得到△BCD，
∴CD=AO=3，
在△OCD中，CD=3，OD=4，OC=5，
∵3²+4²=5²，
∴CD²+OD²=OC²，
∴△OCD為直角三角形，∠ODC=90°，
∴∠BDC=∠BDO+∠ODC=60°+90°=150°；
（2）OA²+2OB²=OC²時，∠ODC=90°．理由如下：
∵△BAO繞點B順時針旋轉后得到△BCD，
∴∠OBD=∠ABC=90°，BO=BD，CD=AO，
∴△OBD為等腰直角三角形，
∴OD=$\sqrt{2}$OB，
∵當CD²+OD²=OC²時，△OCD為直角三角形，∠ODC=90°，
∴OA²+2OB²=OC²，
∴當OA、OB、OC滿足OA²+2OB²=OC²時，∠ODC=90°．

點評 本題考查了旋轉的性質：對應點到旋轉中心的距離相等；對應點與旋轉中心所連線段的夾角等于旋轉角；旋轉前、后的圖形全等．也考查了等邊三角形的判斷與性質和勾股定理的逆定理．