
分析 (1)設可租用甲種貨車x輛,乙種貨車(8-x)輛,因為要一次性運送,所以所裝的貨物應該不少于60個床架和100套桌椅,根據題目所給的其他條件可列出不等式組.
(2)因為甲種貨車每輛須付運費1200元,乙種貨車要付1000元,所以乙種貨車越多越省錢.選擇方案可算出費用.
解答 解:(1)設可租用甲種貨車x輛,乙種貨車(8-x)輛,依題意有
$\left\{\begin{array}{l}{5x+10(8-x)≥60}\\{20x+10(8-x)≥100}\end{array}\right.$,
解得2≤x≤4.
故甲有3種方案:①甲2輛,乙6輛.
②甲3輛,乙5輛.
③甲4輛,乙4輛.
(2)①種方案最省錢.
1200×2+1000×6=8400(元).
選擇①種方案,運費是8400元.
點評 本題考查了一元一次不等式組的應用以及理解題意能力,關鍵是貨車能把床架和桌椅運走列出不等式組,找出方案,然后根據乙車越多越省錢,求出運費.


科目:初中數學 來源: 題型:解答題
查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,有四張背面相同的紙牌.請你用這四張牌計算“24點”,請列出四個符合要求的不同算式.【可運用加、減、乘、除、乘方(例如數2,6,可列62=36或26=64)運算,可用括號;注意:例如4×(1+2+3)=24與(2+1+3)×4=24只是順序不同,屬同一個算式】.
如圖,有四張背面相同的紙牌.請你用這四張牌計算“24點”,請列出四個符合要求的不同算式.【可運用加、減、乘、除、乘方(例如數2,6,可列62=36或26=64)運算,可用括號;注意:例如4×(1+2+3)=24與(2+1+3)×4=24只是順序不同,屬同一個算式】.查看答案和解析>>
科目:初中數學 來源: 題型:解答題
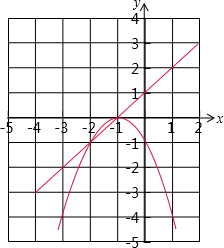 設函數y=(x+1)[(k-2)x+(2k-3)](k是常數).
設函數y=(x+1)[(k-2)x+(2k-3)](k是常數).查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 如圖,點A,B在⊙O上,點C在⊙O外,連接AB和OC交于D,且OB⊥OC,AC=CD.
如圖,點A,B在⊙O上,點C在⊙O外,連接AB和OC交于D,且OB⊥OC,AC=CD. 查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com